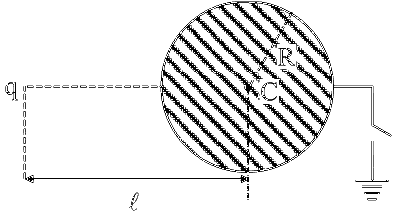
Before grounding

$$ \begin{aligned} & \mathrm{V}_{\text {sphere }}=\left(\mathrm{V}_{\mathrm{C}}\right)_{\text {net }}=\left(\mathrm{V}_{\mathrm{C}}\right)_{\mathrm{q}}+\left(\mathrm{V}_{\mathrm{C}}\right)_{\text {ind }} \\ & \mathrm{V}_{\text {sphere }}=\frac{\mathrm{kq}}{\ell}+0=\frac{9 \times 10^9 \times 10^{-8}}{0.2}=\frac{90}{0.2}=\frac{900}{2}=450 \text { volt } \end{aligned} $$

After grounding

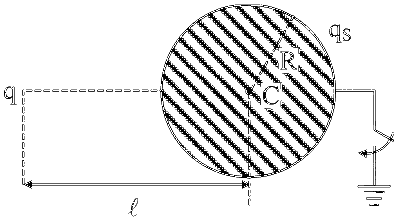
$$ \begin{aligned} & \frac{\mathrm{kQ}}{\ell}+\frac{\mathrm{kq}_{\mathrm{s}}}{\mathrm{R}}=\mathrm{V}_{\text {sphere }}^{\prime}=0 \\ & \mathrm{q}_{\mathrm{s}}=-\frac{\mathrm{R}}{\ell} \mathrm{q}=-\frac{1}{2} \times 10^{-8}=-5 \times 10^{-9} \\ & \mathrm{q}_{\mathrm{s}}=-5 \times 10^{-9} \text { Coulomb } \end{aligned} $$

Charge flower from sphere to ground $=5 \times 10^{-9}$ Coulomb

After grounding is removed

$$ \begin{aligned} & \left(\mathrm{V}_{\text {sphere }}\right)_{\text {final }}=\frac{\mathrm{kq}}{\ell^{\prime}}+\frac{\mathrm{kq}_{\mathrm{s}}}{\mathrm{R}} \\ & =\frac{9 \times 10^9 \times 10^2 \times 10^{-8}}{30}-\frac{9 \times 10^9 \times 5 \times 10^{-9} \times 10^2}{10} \\ & =\frac{9 \times 1000}{30}-450=300 \mathrm{volt}-450 \mathrm{volt}=-150 \mathrm{volt} \end{aligned} $$