JEE Advance - Physics (2025 - Paper 2 Online - No. 3)
As shown in the figures, a uniform rod OO' of length l is hinged at the point O and held in place vertically between two walls using two massless springs of same spring constant. The springs are connected at the midpoint and at the top-end (O') of the rod, as shown in Fig. 1 and the rod is made to oscillate by a small angular displacement. The frequency of oscillation of the rod is f₁. On the other hand, if both the springs are connected at the midpoint of the rod, as shown in Fig. 2 and the rod is made to oscillate by a small angular displacement, then the frequency of oscillation is f₂. Ignoring gravity and assuming motion only in the plane of the diagram, the value of $ \frac{f_1}{f_2} $ is:
Explanation
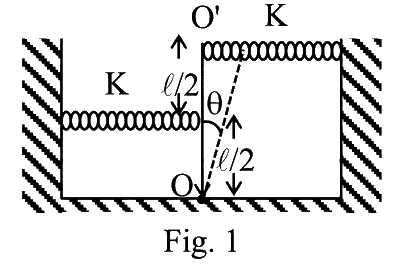
$\begin{aligned} & \frac{\mathrm{ML}^2}{3} \ddot{\theta}+\mathrm{K} \cdot \frac{\ell}{2} \theta \cdot \frac{\ell}{2}+\mathrm{K} \cdot \ell \cdot \theta \cdot \ell=0 \\ & \ddot{\theta}+\frac{15}{4} \frac{\mathrm{k}}{\mathrm{M}} \theta=0 \\ & \ddot{\theta}=-\left(\frac{15}{4} \frac{\mathrm{k}}{\mathrm{M}}\right) \theta \\ & \omega_1=\sqrt{\frac{15 \mathrm{~K}}{4 \mathrm{M}}}\end{aligned}$
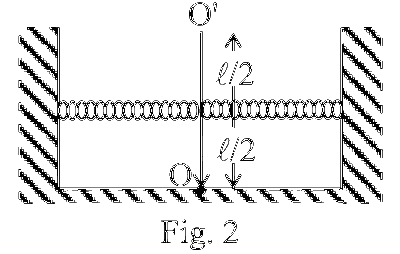
$\frac{1}{3} \mathrm{ML}^2 \ddot{\theta}+2 \mathrm{~K} \frac{\mathrm{~L}}{2} \theta \cdot \frac{\mathrm{~L}}{2}=0$
$\begin{aligned} & \ddot{\theta}+\frac{3}{2} \frac{K}{M} \theta=0 \\ & \ddot{\theta}=-\frac{3}{2} \frac{K}{M} \theta \\ & \omega_2=\sqrt{\frac{3}{2} \frac{K}{M}} \\ & \frac{\omega_1}{\omega_2}=\sqrt{\frac{15}{4} \times \frac{2}{3}}=\sqrt{\frac{5}{2}}\end{aligned}$
Comments (0)


