JEE Advance - Physics (2025 - Paper 2 Online - No. 2)
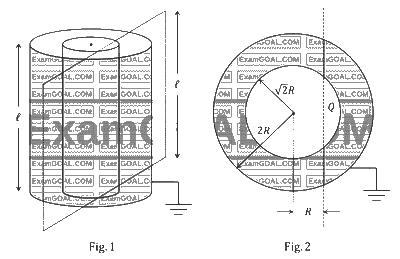
Two co-axial conducting cylinders of same length $\ell$ with radii $\sqrt{2}R$ and $2R$ are kept, as shown in Fig. 1. The charge on the inner cylinder is $Q$ and the outer cylinder is grounded. The annular region between the cylinders is filled with a material of dielectric constant $\kappa=5$. Consider an imaginary plane of the same length $\ell$ at a distance $R$ from the common axis of the cylinders. This plane is parallel to the axis of the cylinders. The cross-sectional view of this arrangement is shown in Fig. 2. Ignoring edge effects, the flux of the electric field through the plane is ($\epsilon_0$ is the permittivity of free space):
Explanation
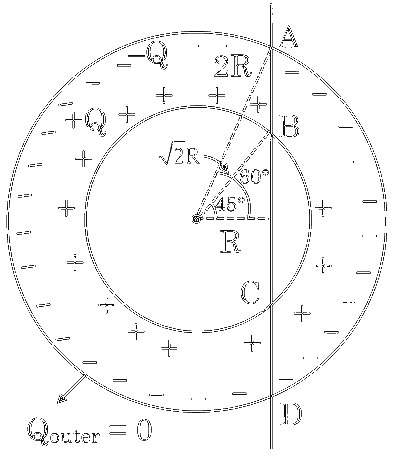
Here we are assuming that " $\ell$ " is very large just for the sake of symmetry. Outside cylinder will have zero electric field inside, so the flux generated on the plate will be due to inner cylinder only in sections AB and CD , as section be will be at that place where electric field is zero.
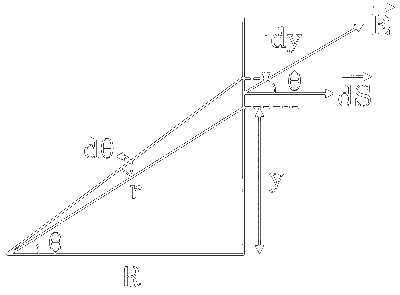
Flux through element will be =
$$ \begin{aligned} \mathrm{d} \phi & =\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{dS}} \\ \mathrm{~d} \phi & =\frac{2 \mathrm{k} \lambda}{\mathrm{r}} \mathrm{dy} \cdot \ell \cdot \cos \theta .........(1) \end{aligned} $$
from figure we can say that
$$ \begin{aligned} & \cos \theta=\frac{R}{r} \Rightarrow r=R \sec \theta \\ & \tan \theta=\frac{y}{R} \Rightarrow y=R \tan \theta \\ & \Rightarrow d y=R \sec ^2 \theta d \theta \\ & d \phi=\frac{2 k \lambda}{R \sec \theta} R \cdot \sec ^2 \theta \cdot \ell \cdot \cos \theta d \theta \\ & d \phi=2 k \lambda \ell d q \end{aligned} $$
$\begin{aligned} & \int_0^{\phi_{\mathrm{AB}}} \mathrm{d} \phi=2 \mathrm{k} \lambda \ell \int_{\pi / 4}^{\pi / 3} \mathrm{~d} \theta \\ & \phi_{\mathrm{AB}}=2 \mathrm{k} \lambda \ell\left[\frac{\pi}{3}-\frac{\pi}{4}\right] \\ & \phi_{\mathrm{AB}}=2 \mathrm{kQ}\left[\frac{\pi}{12}\right] \\ & \phi_{\mathrm{AB}}=2 \times \frac{1}{4 \pi \epsilon_0 \epsilon_{\mathrm{r}}} \mathrm{Q}\left[\frac{\pi}{12}\right] \\ & \phi_{\mathrm{AB}}=\frac{\mathrm{Q}}{120 \epsilon_0} \\ & \phi_{\text {plate }}=\phi_{\mathrm{AB}}+\phi_{\mathrm{BC}}+\phi_{\mathrm{CD}} \quad\left(\phi_{\mathrm{CD}}=\phi_{\mathrm{AB}}\right) \\ & \phi_{\text {plate }}=\frac{\mathrm{Q}}{60 \epsilon_0}\end{aligned}$
Comments (0)


