JEE Advance - Physics (2025 - Paper 2 Online - No. 11)
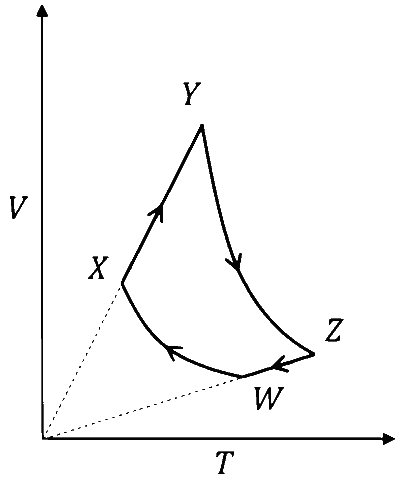
Explanation
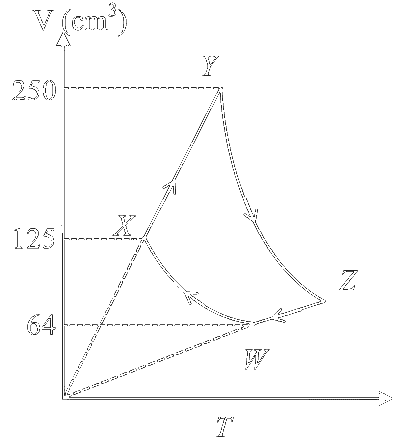
$$ \begin{aligned} & \mathrm{nRT}_{\mathrm{w}}=\mathrm{P}_{\mathrm{w}} \mathrm{~V}_{\mathrm{w}}=1 \mathrm{~J} \\ & \mathrm{P}_{\mathrm{W}}=\frac{1}{64} \times 10^6 \mathrm{~Pa} \end{aligned} $$
For WX process
$$ \begin{aligned} & P_X V_X^y=P_W V_W^y \\ & \Rightarrow P_X=P_W\left(\frac{V_W}{V_X}\right)^y \end{aligned} $$
amount of heat absorbed in XY process
$$ \begin{aligned} \mathrm{Q} & =\mathrm{nCP} \Delta \mathrm{~T}=\mathrm{n} \times \frac{5}{2} \mathrm{R} \times\left[\mathrm{T}_{\mathrm{Y}}-\mathrm{T}_{\mathrm{X}}\right] \quad\left[\text { For monoatomic gas } \mathrm{C}_{\mathrm{P}}=\frac{5 \mathrm{R}}{2}\right] \\ \mathrm{Q} & =\frac{5}{2}\left[\mathrm{nRT}_{\mathrm{Y}}-\mathrm{nRT}_{\mathrm{X}}\right] \\ & =\frac{5}{2}\left[\mathrm{P}_{\mathrm{Y}} \mathrm{~V}_{\mathrm{Y}}-\mathrm{P}_{\mathrm{X}} \mathrm{~V}_{\mathrm{X}}\right] \\ & =\frac{5}{2} \mathrm{P}_{\mathrm{X}}\left[\mathrm{~V}_{\mathrm{Y}}-\mathrm{V}_{\mathrm{X}}\right] \quad\left[\because \mathrm{P}_{\mathrm{X}}=\mathrm{P}_{\mathrm{Y}} ; \text { Isobaric process }\right] \\ & =\frac{5}{2} \times \mathrm{P}_{\mathrm{W}} \times\left[\frac{\mathrm{V}_{\mathrm{W}}}{\mathrm{~V}_{\mathrm{X}}}\right]^{\mathrm{y}}\left[\mathrm{~V}_{\mathrm{Y}}-\mathrm{V}_{\mathrm{X}}\right] \end{aligned} $$
Putting values :
Q = 1.6 Joule
Comments (0)


