JEE Advance - Physics (2024 - Paper 1 Online - No. 17)
The circuit shown in the figure contains an inductor $L$, a capacitor $C_0$, a resistor $R_0$ and an ideal battery. The circuit also contains two keys $\mathrm{K}_1$ and $\mathrm{K}_2$. Initially, both the keys are open and there is no charge on the capacitor. At an instant, key $\mathrm{K}_1$ is closed and immediately after this the current in $R_0$ is found to be $I_1$. After a long time, the current attains a steady state value $I_2$. Thereafter, $\mathrm{K}_2$ is closed and simultaneously $\mathrm{K}_1$ is opened and the voltage across $C_0$ oscillates with amplitude $V_0$ and angular frequency $\omega_0$.

Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) The value of $I_1$ in Ampere is | (1) $0$ |
| (Q) The value of $I_2$ in Ampere is | (2) $2$ |
| (R) The value of $\omega_0$ in kilo-radians/s is | (3) $4$ |
| (S) The value of $V_0$ in Volt is | (4) $20$ |
| (5) $200$ |
Explanation
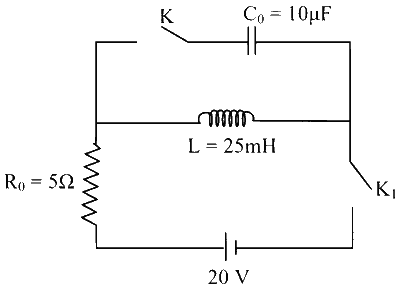
(P) When $$K_1$$ is closed current in $$R_0$$ is $$I_1$$
At $$\mathrm{t}=0$$; circuit will be
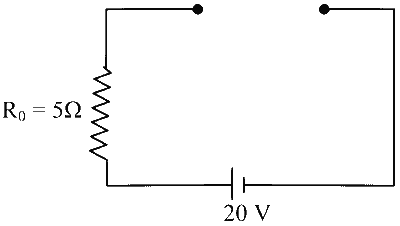
$$\begin{aligned} & \mathrm{I}_1=0 \\ & \mathrm{P} \rightarrow(1) \end{aligned}$$
(Q) After long time inductor behave as a wire so $$I_2$$
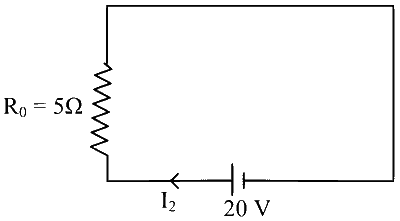
$$\begin{aligned} & \mathrm{I}_2=\frac{20}{5}=4 \mathrm{~A} \\ & \mathrm{Q} \rightarrow(3) \end{aligned}$$
$$\text { (R) When } K_2 \text { is closed and } K_1 \text { open }$$
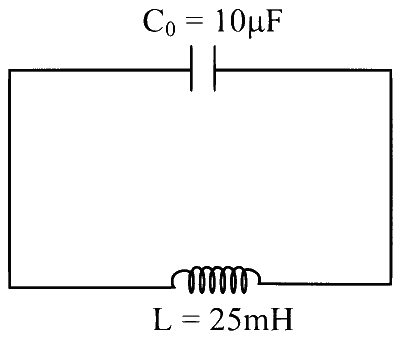
$$\begin{aligned} & \omega_0=\frac{1}{\sqrt{\mathrm{LC}}} \\ & \omega_0=\frac{1}{\sqrt{25 \times 10^{-3} \times 10 \times 10^{-6}}}=\frac{1}{5 \times 10^{-4}} \\ & \omega_0=2 \times 10^3 \mathrm{rad} / \mathrm{s} \\ & \omega_0=2 \mathrm{kilo}-\mathrm{radian} / \mathrm{s} \\ & \mathrm{R} \rightarrow(2) \end{aligned}$$
(S) Now $$K_2$$ is closed and $$K_1$$ open
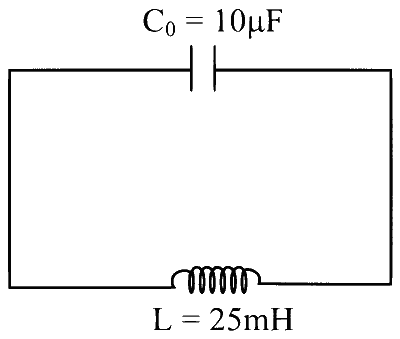
$$\begin{aligned} & \frac{1}{2} \mathrm{LI}_2^2=\frac{1}{2} \mathrm{CV}_0^2 \\ & 25 \times 10^{-3} \times(4)^2=10 \times 10^{-6} \times \mathrm{V}_0^2 \\ & \mathrm{~V}_0^2=2500 \times 16 \\ & \mathrm{~V}_0=50 \times 4=200 \mathrm{~V} \\ & \mathrm{~S} \rightarrow(5) \end{aligned}$$
Comments (0)


