JEE Advance - Physics (2024 - Paper 1 Online - No. 16)
A light ray is incident on the surface of a sphere of refractive index $n$ at an angle of incidence $\theta_0$. The ray partially refracts into the sphere with angle of refraction $\phi_0$ and then partly reflects from the back surface. The reflected ray then emerges out of the sphere after a partial refraction. The total angle of deviation of the emergent ray with respect to the incident ray is $\alpha$. Match the quantities mentioned in List-I with their values in List-II and choose the correct option.
| List-I | List-II |
|---|---|
| (P) If $n = 2$ and $\alpha = 180^\circ$, then all the possible values of $\theta_0$ will be | (1) $30^\circ$ and $0^\circ$ |
| (Q) If $n = \sqrt{3}$ and $\alpha = 180^\circ$, then all the possible values of $\theta_0$ will be | (2) $60^\circ$ and $0^\circ$ |
| (R) If $n = \sqrt{3}$ and $\alpha = 180^\circ$, then all the possible values of $\phi_0$ will be | (3) $45^\circ$ and $0^\circ$ |
| (S) If $n = \sqrt{2}$ and $\theta_0 = 45^\circ$, then all the possible values of $\alpha$ will be | (4) $150^\circ$ |
| (5) $0^\circ$ |
Explanation
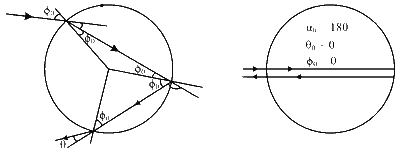
$$\begin{aligned} &\begin{aligned} & \alpha=\left(\theta_0-\phi_0\right)+\left(180-2 \phi_0\right)+\left(\theta_0-2 \phi_0\right) \\ & \alpha=180+2 \theta_0-4 \phi_0 \end{aligned}\\ &\begin{aligned} & \text { (P) } \alpha=180+2 \theta_0-4 \phi_0 \\ & 180=180+2 \theta_0-4 \phi_0 \Rightarrow \theta_0=2 \phi_0 \quad \text{... (i}\\ & \sin \theta_0=2 \sin \phi_0 \quad \text{... (ii} \end{aligned} \end{aligned}$$
From (i) & (ii)
$$\begin{aligned} & \sin \theta_0=2 \sin \left(\theta_0 / 2\right) \Rightarrow \cos \left(\frac{\theta_0}{2}\right)=1 \\ & \frac{\theta_0}{2}=0 \\ & \Rightarrow \theta_0=0 \end{aligned}$$
$$\begin{aligned} & \text { (Q) } \theta_0=2 \phi_0 \quad \text{... (i)}\\ & \sin \theta_0=\sqrt{3} \sin \phi_0 \quad \text{... (ii)} \end{aligned}$$
From (i) & (ii)
$$\begin{aligned} & \sin \theta_0=\sqrt{3} \sin \left(\frac{\theta_0}{2}\right) \\ & \Rightarrow \cos \left(\frac{\theta_0}{2}\right)=\frac{\sqrt{3}}{2} \\ & \frac{\theta_0}{2}=30,150 \\ & \theta_0=60,300 \text { (Rejected) } \\ & \theta_0=60 \& 0 \end{aligned}$$
$$\begin{aligned} & \text { (R) } \theta_0=2 \phi_0 \\ & \sin \theta_0=\sqrt{3} \sin \phi_0 \\ & \sin 2 \theta_0=\sqrt{3} \sin \phi_0 \\ & \cos \phi_0=\frac{\sqrt{3}}{2} \\ & \phi_0=30,150 \text { (Rejected) } \end{aligned}$$
$$\begin{aligned} & \phi_0=30 \& 0 \quad \text{... (i)}\\ & (S) \sin 45=\sqrt{2} \cos \phi_0 \\ & \cos \phi_0=1 / 2 \\ & \phi_0=60 \\ & \alpha=180+2 \theta_0-4 \phi_0 \end{aligned}$$
$$\begin{aligned} & \alpha=180+90-120 \quad \text{... (iv)}\\ & =180-30 ; \alpha=150^{\circ} \end{aligned}$$
Comments (0)


