JEE Advance - Physics (2023 - Paper 2 Online - No. 9)
A rectangular conducting loop of length $4 \mathrm{~cm}$ and width $2 \mathrm{~cm}$ is in the $x y$-plane, as shown in the figure. It is being moved away from a thin and long conducting wire along the direction $\frac{\sqrt{3}}{2} \hat{x}+\frac{1}{2} \hat{y}$ with a constant speed $\mathrm{v}$. The wire is carrying a steady current $I=10 \mathrm{~A}$ in the positive $x$-direction. A current of $10 \mu \mathrm{A}$ flows through the loop when it is at a distance $d=4 \mathrm{~cm}$ from the wire. If the resistance of the loop is $0.1 \Omega$, then the value of $\mathrm{v}$ is ________ $\mathrm{m} \mathrm{s}^{-1}$.
[Given: The permeability of free space $\mu_0=4 \pi \times 10^{-7} \mathrm{~N} \mathrm{~A}^{-2}$ ]

[Given: The permeability of free space $\mu_0=4 \pi \times 10^{-7} \mathrm{~N} \mathrm{~A}^{-2}$ ]

Answer
4
Explanation
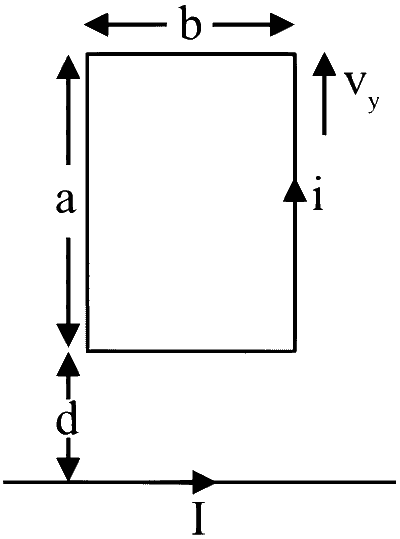
$$ \begin{aligned} &R=0.1 \Omega\\\\ &\varepsilon=\left(\mathrm{B}_1-\mathrm{B}_2\right) b v_{\mathrm{y}}\\\\ &\begin{aligned} & \mathrm{i}=\frac{\varepsilon}{R}=\frac{\mu_0 I}{2 \pi R}\left(\frac{1}{d}-\frac{1}{d+a}\right) b v_y \\\\ & \Rightarrow 10^{-5}=\frac{2 \times 10^{-7} \times 10}{0.1}\left[\frac{1}{4}-\frac{1}{8}\right] \times 2 . v_y \end{aligned} \end{aligned} $$
$$ \therefore \mathrm{v}_{\mathrm{y}}=2 $$
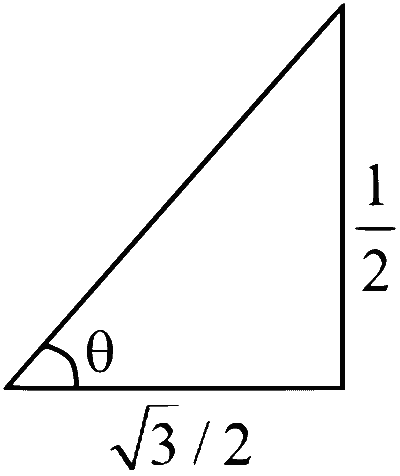
$$ \begin{aligned} & \tan \theta=\frac{\mathrm{v}_{\mathrm{y}}}{\mathrm{v}_{\mathrm{x}}}=\frac{1}{\sqrt{3}} \\\\ & \therefore \mathrm{v}_{\mathrm{x}}=2 \sqrt{3} \\\\ & \therefore \mathrm{v}=\sqrt{\mathrm{v}_{\mathrm{x}}^2+\mathrm{v}_{\mathrm{y}}^2}=4 \end{aligned} $$
Comments (0)


