JEE Advance - Physics (2023 - Paper 2 Online - No. 8)
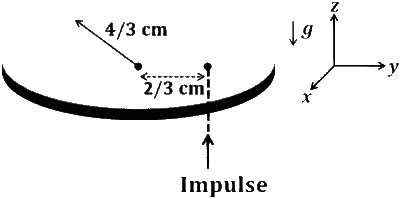
A thin circular coin of mass $5 \mathrm{gm}$ and radius $4 / 3 \mathrm{~cm}$ is initially in a horizontal $x y$-plane. The coin is tossed vertically up ( $+z$ direction) by applying an impulse of $\sqrt{\frac{\pi}{2}} \times 10^{-2} \mathrm{~N}$-s at a distance $2 / 3 \mathrm{~cm}$ from its center. The coin spins about its diameter and moves along the $+z$ direction. By the time the coin reaches back to its initial position, it completes $n$ rotations. The value of $n$ is ________.
[Given: The acceleration due to gravity $g=10 \mathrm{~m} \mathrm{~s}^{-2}$ ]
[Given: The acceleration due to gravity $g=10 \mathrm{~m} \mathrm{~s}^{-2}$ ]

Answer
30
Explanation
A coin with a radius of $ r = \frac{4}{3} \times 10^{-2} \, \text{m} $ and a mass of $ m = 5 \times 10^{-3} \, \text{kg} $ is thrown upwards. An impulse of $ J_{\text{lin}} = \sqrt{\frac{\pi}{2}} \times 10^{-2} \, \text{N s} $ is applied perpendicularly to the plane of the coin. This impulse is delivered at a distance of $ d = \frac{r}{2} $ from the center of the coin.
Initially at rest, the coin experiences a change in linear momentum due to the applied linear impulse, leading to the equation :
$ m v_{\text{cm}} = J_{\text{lin}} $.
where $ m $ is the mass of the coin, $ v_{\text{cm}} $ is its center of mass velocity after the impulse, and $ J_{\text{lin}} $ is the magnitude of the linear impulse.
After the impulse, the center of mass of the coin ascends with an initial velocity $ v_{\text{cm}} $. Under the influence of gravity, the coin returns to its original position in a time duration expressed by :
$ t = \frac{2 v_{\text{cm}}}{g} = \frac{2 J_{\text{lin}}}{mg} $,
where $ g $ is the acceleration due to gravity, $ J_{\text{lin}} $ is the linear impulse applied, and $ m $ is the mass of the coin.
The coin undergoes rotation about its axis, and the angular impulse exerted on it around its center is described by the equation :
$ J_{\text{ang}} = d J_{\text{lin}} = \left( \frac{r}{2} \right) J_{\text{lin}} $,
where $ J_{\text{ang}} $ is the angular impulse, $ d $ is the distance from the center at which the linear impulse $ J_{\text{lin}} $ is applied, and $ r $ is the radius of the coin.
The angular impulse leads to a change in the angular momentum of the coin about a horizontal axis passing through its center. This relationship is given by :
$ I_{\text{cm}} \omega = L_{\text{ang}} = \left( \frac{r}{2} \right) J_{\text{lin}} $,
where $ I_{\text{cm}} $ is the moment of inertia of the coin about its center of mass, $ \omega $ is the angular velocity after the impulse, and $ L_{\text{ang}} $ is the angular momentum resulting from the angular impulse $ J_{\text{ang}} $.
The angular speed of the coin, denoted as $ \omega $, is determined by the equation :
$ \omega = \frac{(r / 2) J_{\text{lin}}}{I_{\text{cm}}} = \frac{(r / 2) J_{\text{lin}}}{(1 / 4) m r^2} = \frac{2 J_{\text{lin}}}{m r} $,
where $ r $ is the radius of the coin, $ J_{\text{lin}} $ is the linear impulse applied, $ m $ is the mass of the coin, and $ I_{\text{cm}} $ is its moment of inertia about the center of mass.
After tossing, the angular speed of the coin remains constant because there is no external torque. The number of rotations \( n \) completed by the coin during the time \( t \) is calculated as :
$ n = \frac{\theta}{2\pi} = \frac{\omega t}{2\pi} = \frac{2 J_{\text{lin}}^2}{\pi m^2 g r} $
Substituting the given values, it becomes :
$ n = \frac{2 \left( \frac{\pi}{2} \times 10^{-4} \right)}{\pi \left( 5 \times 10^{-3} \right)^2 \times 10 \times \left( \frac{4}{3} \times 10^{-2} \right)} = 30 $.
where $ \theta $ is the total angular displacement, $ \omega $ is the angular speed of the coin, $ J_{\text{lin}} $ is the linear impulse, $ m $ is the mass of the coin, $ g $ is the acceleration due to gravity, and $ r $ is the radius of the coin.
Initially at rest, the coin experiences a change in linear momentum due to the applied linear impulse, leading to the equation :
$ m v_{\text{cm}} = J_{\text{lin}} $.
where $ m $ is the mass of the coin, $ v_{\text{cm}} $ is its center of mass velocity after the impulse, and $ J_{\text{lin}} $ is the magnitude of the linear impulse.
After the impulse, the center of mass of the coin ascends with an initial velocity $ v_{\text{cm}} $. Under the influence of gravity, the coin returns to its original position in a time duration expressed by :
$ t = \frac{2 v_{\text{cm}}}{g} = \frac{2 J_{\text{lin}}}{mg} $,
where $ g $ is the acceleration due to gravity, $ J_{\text{lin}} $ is the linear impulse applied, and $ m $ is the mass of the coin.
The coin undergoes rotation about its axis, and the angular impulse exerted on it around its center is described by the equation :
$ J_{\text{ang}} = d J_{\text{lin}} = \left( \frac{r}{2} \right) J_{\text{lin}} $,
where $ J_{\text{ang}} $ is the angular impulse, $ d $ is the distance from the center at which the linear impulse $ J_{\text{lin}} $ is applied, and $ r $ is the radius of the coin.
The angular impulse leads to a change in the angular momentum of the coin about a horizontal axis passing through its center. This relationship is given by :
$ I_{\text{cm}} \omega = L_{\text{ang}} = \left( \frac{r}{2} \right) J_{\text{lin}} $,
where $ I_{\text{cm}} $ is the moment of inertia of the coin about its center of mass, $ \omega $ is the angular velocity after the impulse, and $ L_{\text{ang}} $ is the angular momentum resulting from the angular impulse $ J_{\text{ang}} $.
The angular speed of the coin, denoted as $ \omega $, is determined by the equation :
$ \omega = \frac{(r / 2) J_{\text{lin}}}{I_{\text{cm}}} = \frac{(r / 2) J_{\text{lin}}}{(1 / 4) m r^2} = \frac{2 J_{\text{lin}}}{m r} $,
where $ r $ is the radius of the coin, $ J_{\text{lin}} $ is the linear impulse applied, $ m $ is the mass of the coin, and $ I_{\text{cm}} $ is its moment of inertia about the center of mass.
After tossing, the angular speed of the coin remains constant because there is no external torque. The number of rotations \( n \) completed by the coin during the time \( t \) is calculated as :
$ n = \frac{\theta}{2\pi} = \frac{\omega t}{2\pi} = \frac{2 J_{\text{lin}}^2}{\pi m^2 g r} $
Substituting the given values, it becomes :
$ n = \frac{2 \left( \frac{\pi}{2} \times 10^{-4} \right)}{\pi \left( 5 \times 10^{-3} \right)^2 \times 10 \times \left( \frac{4}{3} \times 10^{-2} \right)} = 30 $.
where $ \theta $ is the total angular displacement, $ \omega $ is the angular speed of the coin, $ J_{\text{lin}} $ is the linear impulse, $ m $ is the mass of the coin, $ g $ is the acceleration due to gravity, and $ r $ is the radius of the coin.
Comments (0)


