JEE Advance - Physics (2023 - Paper 2 Online - No. 7)
The electric field associated with an electromagnetic wave propagating in a dielectric medium is given by $\vec{E}=30(2 \hat{x}+\hat{y}) \sin \left[2 \pi\left(5 \times 10^{14} t-\frac{10^7}{3} z\right)\right] \mathrm{Vm}^{-1}$. Which of the following option(s) is(are) correct?
[Given: The speed of light in vacuum, $c=3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}$ ]
[Given: The speed of light in vacuum, $c=3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}$ ]
$B_x=-2 \times 10^{-7} \sin \left[2 \pi\left(5 \times 10^{14} t-\frac{10^7}{3} z\right)\right] \mathrm{Wb} \mathrm{m}^{-2}$.
$B_y=2 \times 10^{-7} \sin \left[2 \pi\left(5 \times 10^{14} t-\frac{10^7}{3} z\right)\right] \mathrm{Wb} \mathrm{m}^{-2}$.
The wave is polarized in the $x y$-plane with polarization angle $30^{\circ}$ with respect to the $x$-axis.
The refractive index of the medium is 2.
Explanation
1. Calculation of the Speed of Light in a Medium:
- The speed of light in a medium, denoted as $$ V $$, is given by the formula $$ V = \frac{W}{k} $$.
- Substituting values, we get $$ V = \frac{3 \times 5 \times 10^{14}}{10^7} = 1.5 \times 10^8 \text{ m/s} $$.
2. Determination of the Refractive Index:
- The refractive index, $$ \mu $$, is the ratio of the speed of light in vacuum, $$ C $$, to the speed of light in the medium, $$ V $$.
- Substituting values, $$ \mu = \frac{3 \times 10^8}{1.5 \times 10^8} = 2 $$.
- Hence, the refractive index $$ \mu $$ is 2.
Therefore, the option (D) is the answer.
Given, $\vec{E}=30(2 \hat{x}+\hat{y}) \sin \left[2 \pi\left(5 \times 10^{14} t-\frac{10^7}{3} z\right)\right] \mathrm{Vm}^{-1}$
Now magnitude of
$$ \begin{aligned} B & =\frac{E}{v} \\\\ \Rightarrow B & =\frac{30 \sqrt{5}}{1.5 \times 10^8} \end{aligned} $$
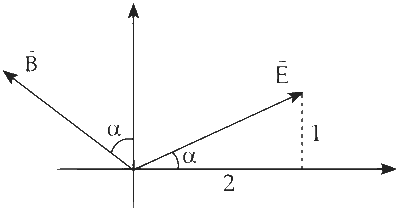
$\begin{aligned} & \tan \alpha=\frac{1}{2} \\\\ & \sin \alpha=\frac{1}{\sqrt{5}}\end{aligned}$
The direction of $\vec{B}$ is along the direction of $\vec{v} \times \vec{E}$
i.e. $\hat{v} \times \hat{E}=\hat{B}$
Now $ B_x=-B \sin \alpha$
$$ \Rightarrow B_x=-\frac{30 \sqrt{5}}{1.5 \times 10^8} \times \frac{1}{\sqrt{5}}=-2 \times 10^7 $$
Therefore, option (A) is the answer.
- The speed of light in a medium, denoted as $$ V $$, is given by the formula $$ V = \frac{W}{k} $$.
- Substituting values, we get $$ V = \frac{3 \times 5 \times 10^{14}}{10^7} = 1.5 \times 10^8 \text{ m/s} $$.
2. Determination of the Refractive Index:
- The refractive index, $$ \mu $$, is the ratio of the speed of light in vacuum, $$ C $$, to the speed of light in the medium, $$ V $$.
- Substituting values, $$ \mu = \frac{3 \times 10^8}{1.5 \times 10^8} = 2 $$.
- Hence, the refractive index $$ \mu $$ is 2.
Therefore, the option (D) is the answer.
Given, $\vec{E}=30(2 \hat{x}+\hat{y}) \sin \left[2 \pi\left(5 \times 10^{14} t-\frac{10^7}{3} z\right)\right] \mathrm{Vm}^{-1}$
Now magnitude of
$$ \begin{aligned} B & =\frac{E}{v} \\\\ \Rightarrow B & =\frac{30 \sqrt{5}}{1.5 \times 10^8} \end{aligned} $$

$\begin{aligned} & \tan \alpha=\frac{1}{2} \\\\ & \sin \alpha=\frac{1}{\sqrt{5}}\end{aligned}$
The direction of $\vec{B}$ is along the direction of $\vec{v} \times \vec{E}$
i.e. $\hat{v} \times \hat{E}=\hat{B}$
Now $ B_x=-B \sin \alpha$
$$ \Rightarrow B_x=-\frac{30 \sqrt{5}}{1.5 \times 10^8} \times \frac{1}{\sqrt{5}}=-2 \times 10^7 $$
Therefore, option (A) is the answer.
Comments (0)


