JEE Advance - Physics (2023 - Paper 2 Online - No. 6)
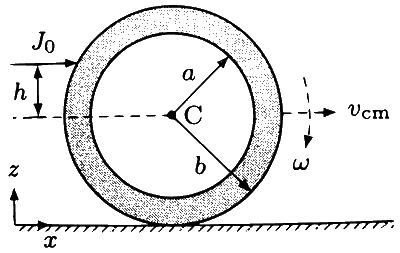
An annular disk of mass $M$, inner radius $a$ and outer radius $b$ is placed on a horizontal surface with coefficient of friction $\mu$, as shown in the figure. At some time, an impulse $J_0 \hat{x}$ is applied at a height $h$ above the center of the disk. If $h=h_m$ then the disk rolls without slipping along the $x$-axis. Which of the following statement(s) is(are) correct?


For $\mu \neq 0$ and $a \rightarrow 0, h_m=b / 2$.
For $\mu \neq 0$ and $a \rightarrow b, h_m=b$.
For $h=h_m$, the initial angular velocity does not depend on the inner radius $a$.
For $\mu=0$ and $h=0$, the wheel always slides without rolling.
Explanation
The moment of inertia $ I_{\text{cm}} $ of an annular disc, with an inner radius $ a $, an outer radius $ b $, and a mass $ m $, about an axis perpendicular to the disc and passing through its center $ C $, is given by :
$ I_{\text{cm}} = \frac{1}{2} m \left( a^2 + b^2 \right) $,
where $ a^2 $ and $ b^2 $ are the squares of the inner and outer radii, respectively.
The linear impulse $ J_0 $ alters the linear momentum of the disc. Right after the impulse is applied, the linear momentum can be represented as :
$ m v_{\text{cm}} = J_0 $,
where $ m $ is the mass of the disc and $ v_{\text{cm}} $ is the velocity of the center of mass resulting from the impulse.
The angular impulse about the center of mass $ C $ of the disc is applied in a clockwise direction, with its magnitude being $ J_{0, \text{ang}} = h J_0 $. This impulse changes the angular momentum of the disc about point $ C $, expressed as :
$ I_{\text{cm}} \omega = J_{0, \text{ang}} = h J_0 $,
where $ I_{\text{cm}} $ is the moment of inertia of the disc about its center of mass, $ \omega $ is the angular velocity resulting from the angular impulse, $ J_0 $ is the linear impulse, and $ h $ is a factor relating the angular impulse to the linear impulse.
For the disc to roll without slipping, given that the friction coefficient $ \mu $ is non-zero, the condition is $ v_{\text{cm}} = \omega b $. By substituting the expressions for $ v_{\text{cm}} $ and $ \omega $ and solving, we obtain the following relationship for the minimum value of $ h $ (denoted as $ h_m $) :
$ h_m = \frac{I_{\text{cm}}}{mb} = \frac{a^2 + b^2}{2b} $,
where $ I_{\text{cm}} $ is the moment of inertia of the disc about its center of mass, $ m $ is the mass of the disc, $ a $ is the inner radius, and $ b $ is the outer radius of the disc.
By substituting $ a = 0 $ into the formula, we find that $ h_m = \frac{b}{2} $. This implies that a solid disc will roll without slipping if the impulse is applied midway along the upper half of the disc.
Similarly, substituting $ a = b $ yields $ h_m = b $. This indicates that a ring (an annular disc with equal inner and outer radii) will roll without slipping when the horizontal impulse is applied at the very top of the ring.
For the condition where $ h = h_m $, the initial angular velocity $ \omega $ is given by :
$ \omega = \frac{h_m J_0}{I_{\text{cm}}} = \frac{J_0}{mb} $.
This expression for the angular velocity is independent of the inner radius $ a $ of the disc.
When a wheel is placed on a smooth surface with no friction ($\mu = 0$) and an impulse is applied directly at its center ($h = 0$), there is no torque generated to initiate rotation. Consequently, under these conditions, if an impulse is delivered to the center of a wheel on a frictionless surface, the wheel will invariably slide and not roll.
$ I_{\text{cm}} = \frac{1}{2} m \left( a^2 + b^2 \right) $,
where $ a^2 $ and $ b^2 $ are the squares of the inner and outer radii, respectively.

The linear impulse $ J_0 $ alters the linear momentum of the disc. Right after the impulse is applied, the linear momentum can be represented as :
$ m v_{\text{cm}} = J_0 $,
where $ m $ is the mass of the disc and $ v_{\text{cm}} $ is the velocity of the center of mass resulting from the impulse.
The angular impulse about the center of mass $ C $ of the disc is applied in a clockwise direction, with its magnitude being $ J_{0, \text{ang}} = h J_0 $. This impulse changes the angular momentum of the disc about point $ C $, expressed as :
$ I_{\text{cm}} \omega = J_{0, \text{ang}} = h J_0 $,
where $ I_{\text{cm}} $ is the moment of inertia of the disc about its center of mass, $ \omega $ is the angular velocity resulting from the angular impulse, $ J_0 $ is the linear impulse, and $ h $ is a factor relating the angular impulse to the linear impulse.
For the disc to roll without slipping, given that the friction coefficient $ \mu $ is non-zero, the condition is $ v_{\text{cm}} = \omega b $. By substituting the expressions for $ v_{\text{cm}} $ and $ \omega $ and solving, we obtain the following relationship for the minimum value of $ h $ (denoted as $ h_m $) :
$ h_m = \frac{I_{\text{cm}}}{mb} = \frac{a^2 + b^2}{2b} $,
where $ I_{\text{cm}} $ is the moment of inertia of the disc about its center of mass, $ m $ is the mass of the disc, $ a $ is the inner radius, and $ b $ is the outer radius of the disc.
By substituting $ a = 0 $ into the formula, we find that $ h_m = \frac{b}{2} $. This implies that a solid disc will roll without slipping if the impulse is applied midway along the upper half of the disc.
Similarly, substituting $ a = b $ yields $ h_m = b $. This indicates that a ring (an annular disc with equal inner and outer radii) will roll without slipping when the horizontal impulse is applied at the very top of the ring.
For the condition where $ h = h_m $, the initial angular velocity $ \omega $ is given by :
$ \omega = \frac{h_m J_0}{I_{\text{cm}}} = \frac{J_0}{mb} $.
This expression for the angular velocity is independent of the inner radius $ a $ of the disc.
When a wheel is placed on a smooth surface with no friction ($\mu = 0$) and an impulse is applied directly at its center ($h = 0$), there is no torque generated to initiate rotation. Consequently, under these conditions, if an impulse is delivered to the center of a wheel on a frictionless surface, the wheel will invariably slide and not roll.
Comments (0)


