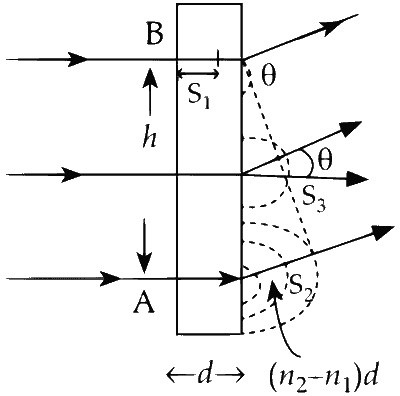
At point A on one end of the slab, the wavefront takes a time $$ t $$ to reach the other end. The time $$ t $$ can be expressed as the ratio of the distance traveled, $$ d $$, to the speed of the wave in the medium, which is $$ \frac{c}{n_1} $$ (where $$ c $$ is the speed of light in vacuum and $$ n_1 $$ is the refractive index of the medium at A). Therefore, the time taken $$ t $$ is given by $$ t = \frac{d}{\frac{c}{n_1}} = \frac{n_1 d}{c} $$.

Simultaneously, consider the wavefront at point B, located in a different medium with a refractive index $$ n_2 $$. In the same time $$ t $$, the wavefront at B travels a distance $$ s_1 $$. The distance $$ s_1 $$ can be calculated as the product of the speed of light in the medium at B, $$ \frac{c}{n_2} $$, and the time $$ t $$, yielding $$ s_1 = \frac{c}{n_2} \times \frac{n_1 d}{c} = \frac{d n_1}{n_2} $$.

Once the wavefront at B reaches the end of the slab, an additional time $$ t_1 $$ elapses. The time $$ t_1 $$ can be determined by considering the remaining distance the wavefront must travel in the slab, which is $$ d - s_1 $$, and dividing it by the speed of light in the medium at B. This gives us $$ t_1 = \left(\frac{d - s_1}{c}\right) n_2 = \left(d - \frac{d n_1}{n_2}\right) \frac{n_2}{c} = \frac{d(n_2 - n_1)}{c} $$.

During this time $$ t_1 $$, the wavefront at A will travel a distance $$ s_2 $$. The distance $$ s_2 $$ is simply the speed of light in vacuum multiplied by the time $$ t_1 $$, leading to $$ s_2 = c t_1 = d(n_2 - n_1) $$.

Finally, the angle $$ \theta $$ can be determined using the tangent function, where $$ \tan \theta $$ is the ratio of the difference in distances traveled by the wavefronts in the two media to the height $$ h $$ of the slab.

Therefore, $$ \tan \theta = \frac{(n_2 - n_1) d}{h} $$.