Sign In

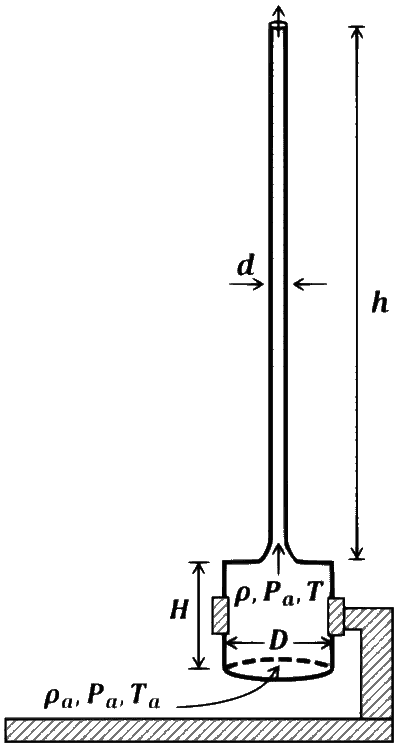
JEE Advance - Physics (2023 - Paper 2 Online - No. 17)

A cylindrical furnace has height $(H)$ and diameter $(D)$ both $1 \mathrm{~m}$. It is maintained at temperature $360 \mathrm{~K}$. The air gets heated inside the furnace at constant pressure $P_a$ and its temperature becomes $T=360 \mathrm{~K}$. The hot air with density $\rho$ rises up a vertical chimney of diameter $d=0.1 \mathrm{~m}$ and height $h=9 \mathrm{~m}$ above the furnace and exits the chimney (see the figure). As a result, atmospheric air of density $\rho_a=$ $1.2 \mathrm{~kg} \mathrm{~m}^{-3}$, pressure $P_a$ and temperature $T_a=300 \mathrm{~K}$ enters the furnace. Assume air as an ideal gas, neglect the variations in $\rho$ and $T$ inside the chimney and the furnace. Also ignore the viscous effects.

[Given: The acceleration due to gravity $g=10 \mathrm{~m} \mathrm{~s}^{-2}$ and $\pi=3.14$ ]

A cylindrical furnace has height $(H)$ and diameter $(D)$ both $1 \mathrm{~m}$. It is maintained at temperature $360 \mathrm{~K}$. The air gets heated inside the furnace at constant pressure $P_a$ and its temperature becomes $T=360 \mathrm{~K}$. The hot air with density $\rho$ rises up a vertical chimney of diameter $d=0.1 \mathrm{~m}$ and height $h=9 \mathrm{~m}$ above the furnace and exits the chimney (see the figure). As a result, atmospheric air of density $\rho_a=$ $1.2 \mathrm{~kg} \mathrm{~m}^{-3}$, pressure $P_a$ and temperature $T_a=300 \mathrm{~K}$ enters the furnace. Assume air as an ideal gas, neglect the variations in $\rho$ and $T$ inside the chimney and the furnace. Also ignore the viscous effects.

[Given: The acceleration due to gravity $g=10 \mathrm{~m} \mathrm{~s}^{-2}$ and $\pi=3.14$ ]

A cylindrical furnace has height $(H)$ and diameter $(D)$ both $1 \mathrm{~m}$. It is maintained at temperature $360 \mathrm{~K}$. The air gets heated inside the furnace at constant pressure $P_a$ and its temperature becomes $T=360 \mathrm{~K}$. The hot air with density $\rho$ rises up a vertical chimney of diameter $d=0.1 \mathrm{~m}$ and height $h=9 \mathrm{~m}$ above the furnace and exits the chimney (see the figure). As a result, atmospheric air of density $\rho_a=$ $1.2 \mathrm{~kg} \mathrm{~m}^{-3}$, pressure $P_a$ and temperature $T_a=300 \mathrm{~K}$ enters the furnace. Assume air as an ideal gas, neglect the variations in $\rho$ and $T$ inside the chimney and the furnace. Also ignore the viscous effects.

[Given: The acceleration due to gravity $g=10 \mathrm{~m} \mathrm{~s}^{-2}$ and $\pi=3.14$ ]

When the chimney is closed using a cap at the top, a pressure difference $\Delta P$ develops between the top and the bottom surfaces of the cap. If the changes in the temperature and density of the hot air, due to the stoppage of air flow, are negligible then the value of $\Delta P$ is __________ $\mathrm{N} \mathrm{m}^{-2}$.
Answer
30

Explanation

We know, $$ \begin{aligned} & \mathrm{P_a}=\frac{\rho R \mathrm{T}}{M} \end{aligned} $$

For a gas R and M are constant. So, $$\rho T$$ = Constant (for constant pressure).

The density of hot air inside the furnace is = $$\rho $$

The air gets heated inside the furnace at constant pressure Pa.

$$ \therefore $$ $$ \rho_{\mathrm{a}} \mathrm{T}_{\mathrm{a}}=\rho \mathrm{T} $$

$$ \Rightarrow $$ 1.2 $$ \times $$ 300 = $$\rho $$ $$ \times $$ 360

$$\Rightarrow \rho=1 \mathrm{~kg} / \mathrm{m}^3$$

After chimney is closed,

Pressure at the bottom surface, P1 = Pa - $$\rho $$gh = Pa - (1)(10)(9)

Pressure at the bottom surface, P2 = Pa - $$\rho $$ag(h + H) = Pa - (1.2)(10)(9 + 1)

$$ \therefore $$ Pressure difference $\Delta P$ develops between the top and the bottom surfaces of the cap

= P1 - P2

= Pa - (1)(10)(9) - Pa + (1.2)(10)(9 + 1)

= 120 - 90 = 30

Comments (0)

Advertisement