Sign In

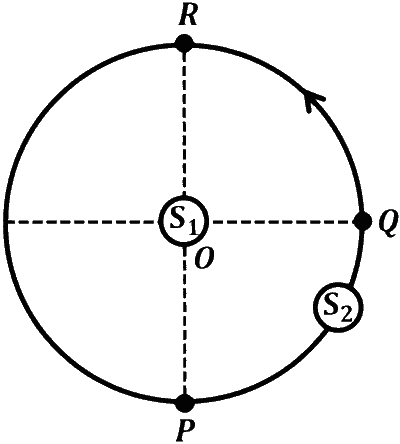
JEE Advance - Physics (2023 - Paper 2 Online - No. 15)

$S_1$ and $S_2$ are two identical sound sources of frequency $656 \mathrm{~Hz}$. The source $S_1$ is located at $O$ and $S_2$ moves anti-clockwise with a uniform speed $4 \sqrt{2} \mathrm{~m} \mathrm{~s}^{-1}$ on a circular path around $O$, as shown in the figure. There are three points $P, Q$ and $R$ on this path such that $P$ and $R$ are diametrically opposite while $Q$ is equidistant from them. A sound detector is placed at point $P$. The source $S_1$ can move along direction $O P$.

[Given: The speed of sound in air is $324 \mathrm{~m} \mathrm{~s}^{-1}$ ]

$S_1$ and $S_2$ are two identical sound sources of frequency $656 \mathrm{~Hz}$. The source $S_1$ is located at $O$ and $S_2$ moves anti-clockwise with a uniform speed $4 \sqrt{2} \mathrm{~m} \mathrm{~s}^{-1}$ on a circular path around $O$, as shown in the figure. There are three points $P, Q$ and $R$ on this path such that $P$ and $R$ are diametrically opposite while $Q$ is equidistant from them. A sound detector is placed at point $P$. The source $S_1$ can move along direction $O P$.

[Given: The speed of sound in air is $324 \mathrm{~m} \mathrm{~s}^{-1}$ ]

$S_1$ and $S_2$ are two identical sound sources of frequency $656 \mathrm{~Hz}$. The source $S_1$ is located at $O$ and $S_2$ moves anti-clockwise with a uniform speed $4 \sqrt{2} \mathrm{~m} \mathrm{~s}^{-1}$ on a circular path around $O$, as shown in the figure. There are three points $P, Q$ and $R$ on this path such that $P$ and $R$ are diametrically opposite while $Q$ is equidistant from them. A sound detector is placed at point $P$. The source $S_1$ can move along direction $O P$.

[Given: The speed of sound in air is $324 \mathrm{~m} \mathrm{~s}^{-1}$ ]

Consider both sources emitting sound. When $S_2$ is at $R$ and $S_1$ approaches the detector with a speed $4 \mathrm{~m} \mathrm{~s}^{-1}$, the beat frequency measured by the detector is _________ $\mathrm{Hz}$.
Answer
8.20

Explanation

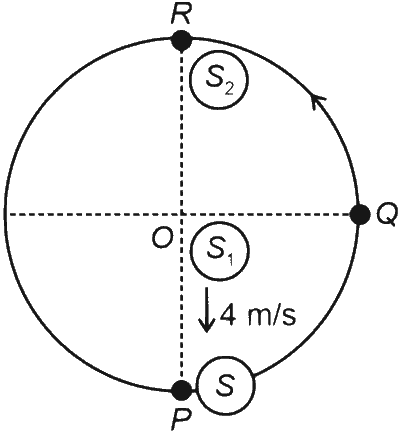
JEE Advanced 2023 Paper 2 Online Physics - Waves Question 3 English Explanation
$$ \begin{aligned} & f_0=656 \mathrm{~Hz} \\\\ & v=324 \mathrm{~m} / \mathrm{s} \end{aligned} $$

Frequency heard due to movement of $\left(S_1\right)$

$$ \begin{aligned} & f_1=\left(\frac{v}{v-u_s}\right) f_0 \\\\ & f_1=\frac{324}{320} \times 656 \end{aligned} $$

And frequency heard due to movement of $\left(S_2\right)$

$$ f_2=656 \mathrm{~Hz} $$

$\therefore$ Beat frequency $\Delta f=f_1-f_2=656\left(\frac{324}{320}-1\right)$

$$ \Rightarrow $$ $$ \Delta f=8.2 $$

Comments (0)

Advertisement