Sign In

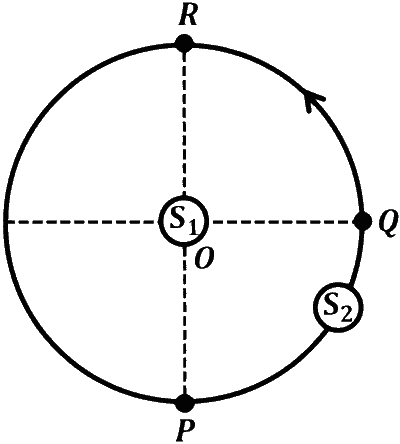
JEE Advance - Physics (2023 - Paper 2 Online - No. 14)

$S_1$ and $S_2$ are two identical sound sources of frequency $656 \mathrm{~Hz}$. The source $S_1$ is located at $O$ and $S_2$ moves anti-clockwise with a uniform speed $4 \sqrt{2} \mathrm{~m} \mathrm{~s}^{-1}$ on a circular path around $O$, as shown in the figure. There are three points $P, Q$ and $R$ on this path such that $P$ and $R$ are diametrically opposite while $Q$ is equidistant from them. A sound detector is placed at point $P$. The source $S_1$ can move along direction $O P$.

[Given: The speed of sound in air is $324 \mathrm{~m} \mathrm{~s}^{-1}$ ]

$S_1$ and $S_2$ are two identical sound sources of frequency $656 \mathrm{~Hz}$. The source $S_1$ is located at $O$ and $S_2$ moves anti-clockwise with a uniform speed $4 \sqrt{2} \mathrm{~m} \mathrm{~s}^{-1}$ on a circular path around $O$, as shown in the figure. There are three points $P, Q$ and $R$ on this path such that $P$ and $R$ are diametrically opposite while $Q$ is equidistant from them. A sound detector is placed at point $P$. The source $S_1$ can move along direction $O P$.

[Given: The speed of sound in air is $324 \mathrm{~m} \mathrm{~s}^{-1}$ ]

$S_1$ and $S_2$ are two identical sound sources of frequency $656 \mathrm{~Hz}$. The source $S_1$ is located at $O$ and $S_2$ moves anti-clockwise with a uniform speed $4 \sqrt{2} \mathrm{~m} \mathrm{~s}^{-1}$ on a circular path around $O$, as shown in the figure. There are three points $P, Q$ and $R$ on this path such that $P$ and $R$ are diametrically opposite while $Q$ is equidistant from them. A sound detector is placed at point $P$. The source $S_1$ can move along direction $O P$.

[Given: The speed of sound in air is $324 \mathrm{~m} \mathrm{~s}^{-1}$ ]

When only $S_2$ is emitting sound and it is at $Q$, the frequency of sound measured by the detector in $\mathrm{Hz}$ is _________.
Answer
648

Explanation

$\begin{gathered}f_0=656 \mathrm{~Hz} \\\\ \text { Velocity of second }=324 \mathrm{~m} \mathrm{~s}^{-1}\end{gathered}$

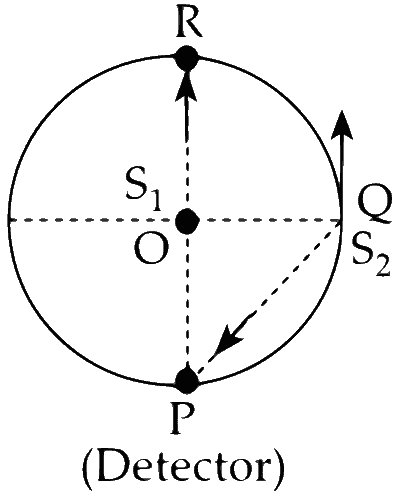
JEE Advanced 2023 Paper 2 Online Physics - Waves Question 4 English Explanation

Velocity of the source away from detector,

$$ \begin{aligned} v_{\mathrm{s}} & =4 \sqrt{2} \cos 45^{\circ}=4 \mathrm{~m} \mathrm{~s}^{-1} \\\\ \therefore \quad f & =\left(\frac{v}{v+v_s}\right) f_0 \\\\ & =\left(\frac{324}{324+4}\right) \times 656=648 \mathrm{~Hz} \end{aligned} $$

Comments (0)

Advertisement