JEE Advance - Physics (2023 - Paper 2 Online - No. 13)
One mole of an ideal gas undergoes two different cyclic processes I and II, as shown in the $P-V$ diagrams below. In cycle I, processes $a, b, c$ and $d$ are isobaric, isothermal, isobaric and isochoric, respectively. In cycle II, processes $a^{\prime}, b^{\prime}, c^{\prime}$ and $d^{\prime}$ are isothermal, isochoric, isobaric and isochoric, respectively. The total work done during cycle $\mathrm{I}$ is $W_I$ and that during cycle II is $W_{I I}$. The ratio $W_I / W_{I I}$ is ________.


Answer
2
Explanation
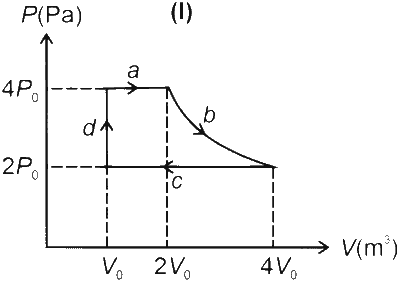
$\begin{aligned} W_1 & =W_a+W_b+W_c+W_d \\\\ & =4 P_0\left(2 V_0-V_0\right)+n R T \ln \left(\frac{4 V_0}{2 V_0}\right)+2 P_0\left(V_0-4 V_0\right)+0 \\\\ & =4 P_0 V_0+n R\left(\frac{8 P_0 V_0}{n R}\right) \ln 2-6 P_0 V_0 \\\\ & =8 P_0 V_0 \ln 2-2 P_0 V_0\end{aligned}$
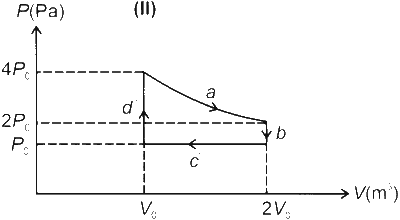
$\begin{aligned} W_{\text {II }} & =W_a^{\prime}+W_b^{\prime}+W_c^{\prime}+W_d^{\prime} \\\\ & =n R T \ln \left(\frac{2 V_0}{V_0}\right)+0+P_0\left(V_0-2 V_0\right)+0 \\\\ & =n R\left(\frac{4 P_0 V_0}{n R}\right) \ln 2-P_0 V_0 \\\\ & =4 P_0 V_0 \ln 2-P_0 V_0\end{aligned}$
$\frac{W_I}{W_{I I}}=\frac{8 P_0 V_0 \ln 2-2 P_0 V_0}{4 P_0 V_0 \ln 2-P_0 V_0}=2$
Comments (0)


