JEE Advance - Physics (2023 - Paper 2 Online - No. 11)
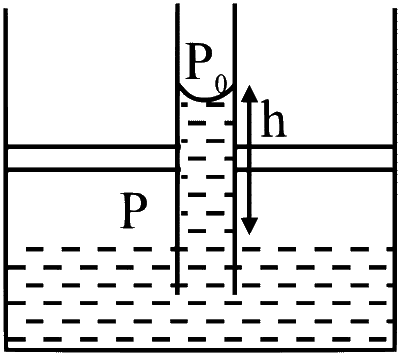
An incompressible liquid is kept in a container having a weightless piston with a hole. A capillary tube of inner radius $0.1 \mathrm{~mm}$ is dipped vertically into the liquid through the airtight piston hole, as shown in the figure. The air in the container is isothermally compressed from its original volume $V_0$ to $\frac{100}{101} V_0$ with the movable piston. Considering air as an ideal gas, the height $(h)$ of the liquid column in the capillary above the liquid level in $\mathrm{cm}$ is _______.
[Given: Surface tension of the liquid is $0.075 \mathrm{~N} \mathrm{~m}^{-1}$, atmospheric pressure is $10^5 \mathrm{~N} \mathrm{~m}^{-2}$, acceleration due to gravity $(\mathrm{g})$ is $10 \mathrm{~m} \mathrm{~s}^{-2}$, density of the liquid is $10^3 \mathrm{~kg} \mathrm{~m}^{-3}$ and contact angle of capillary surface with the liquid is zero]
[Given: Surface tension of the liquid is $0.075 \mathrm{~N} \mathrm{~m}^{-1}$, atmospheric pressure is $10^5 \mathrm{~N} \mathrm{~m}^{-2}$, acceleration due to gravity $(\mathrm{g})$ is $10 \mathrm{~m} \mathrm{~s}^{-2}$, density of the liquid is $10^3 \mathrm{~kg} \mathrm{~m}^{-3}$ and contact angle of capillary surface with the liquid is zero]

Answer
25
Explanation
$$ \begin{aligned} & \mathrm{h}_0=\frac{2 \mathrm{~T} \cos \theta}{\rho \mathrm{gr}}=\frac{2 \times 0.075 \times 1}{10^3 \times 10 \times 10^{-4}}=15 \mathrm{~cm} \\\\ & \mathrm{P}_0 \mathrm{~V}_0=\mathrm{P} \frac{100 \mathrm{~V}_0}{101} \Rightarrow \mathrm{P}=\frac{101}{100} \mathrm{P}_0 \end{aligned} $$
$$ \begin{aligned} & \mathrm{P}_0-\frac{2 \mathrm{~T} \cos \theta}{\mathrm{r}}+\rho \mathrm{gh}=\mathrm{P}=\frac{101}{100} \mathrm{P}_0 \\\\ & \Rightarrow-\rho \mathrm{gh}_0+\rho \mathrm{gh}=\frac{\mathrm{P}_0}{100} \end{aligned} $$
$$ \begin{aligned} & \Rightarrow \mathrm{h}=\mathrm{h}_0+\frac{\mathrm{P}_0}{100 \rho \mathrm{g}} \\\\ & =15 \mathrm{~cm}+\frac{10^5}{100 \times 10^3 \times 10}=25 \mathrm{~cm} \end{aligned} $$
Comments (0)


