JEE Advance - Physics (2023 - Paper 2 Online - No. 1)
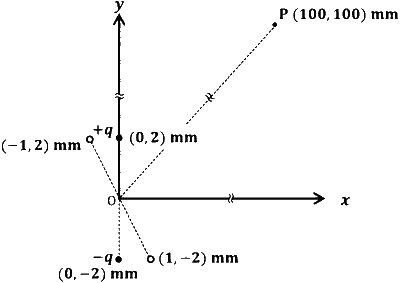
An electric dipole is formed by two charges $+q$ and $-q$ located in $x y$-plane at $(0,2) \mathrm{mm}$ and $(0,-2) \mathrm{mm}$, respectively, as shown in the figure. The electric potential at point $P(100,100) \mathrm{mm}$ due to the dipole is $V_0$. The charges $+q$ and $-q$ are then moved to the points $(-1,2) \mathrm{mm}$ and $(1,-2) \mathrm{mm}$, respectively. What is the value of electric potential at $P$ due to the new dipole?

$\frac{V_0}{4}$
$\frac{V_0}{2}$
$\frac{V_0}{\sqrt{2}}$
$\frac{3 V_0}{4}$
Explanation
$$
V_1 \propto \frac{p_1 \cos \theta_1}{r_1^3}
$$
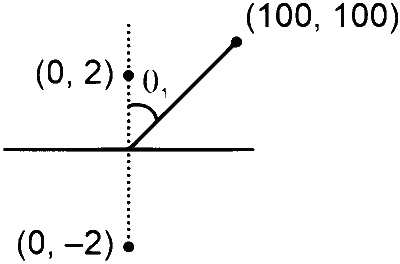
$$ V_2 \propto \frac{p_2 \cos \theta_2}{r_2^3} $$
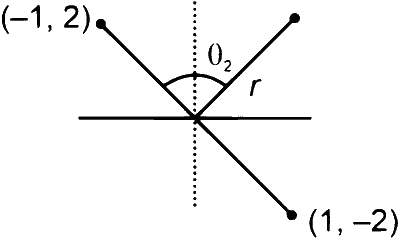
$$ \begin{aligned} & \frac{V_2}{V_1}=\frac{p_2 \cos \theta_2}{p_1 \cos \theta_1} \\\\ & \frac{V_2}{V_1}=\frac{q(-2 \hat{i}+4 \hat{j}) \cdot(\hat{i}+\hat{j})}{q(0 \hat{i}+4 \hat{j}) \cdot(\hat{i}+\hat{j})}=\frac{1}{2} \end{aligned} $$
$$ \Rightarrow V_2=\frac{V_0}{2} $$
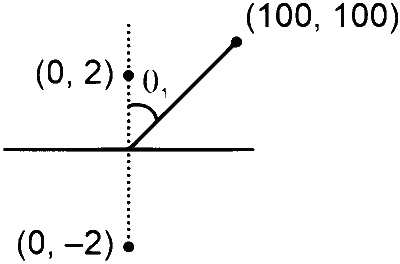
$$ V_2 \propto \frac{p_2 \cos \theta_2}{r_2^3} $$

$$ \begin{aligned} & \frac{V_2}{V_1}=\frac{p_2 \cos \theta_2}{p_1 \cos \theta_1} \\\\ & \frac{V_2}{V_1}=\frac{q(-2 \hat{i}+4 \hat{j}) \cdot(\hat{i}+\hat{j})}{q(0 \hat{i}+4 \hat{j}) \cdot(\hat{i}+\hat{j})}=\frac{1}{2} \end{aligned} $$
$$ \Rightarrow V_2=\frac{V_0}{2} $$
Comments (0)


