JEE Advance - Physics (2022 - Paper 2 Online - No. 9)
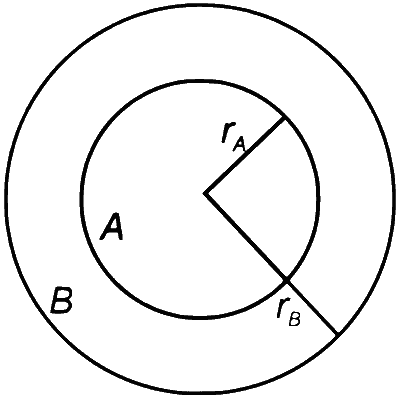
In the figure, the inner (shaded) region $A$ represents a sphere of radius $r_{A}=1$, within which the electrostatic charge density varies with the radial distance $r$ from the center as $\rho_{A}=k r$, where $k$ is positive. In the spherical shell $B$ of outer radius $r_{B}$, the electrostatic charge density varies as $\rho_{B}=$ $\frac{2 k}{r}$. Assume that dimensions are taken care of. All physical quantities are in their SI units.
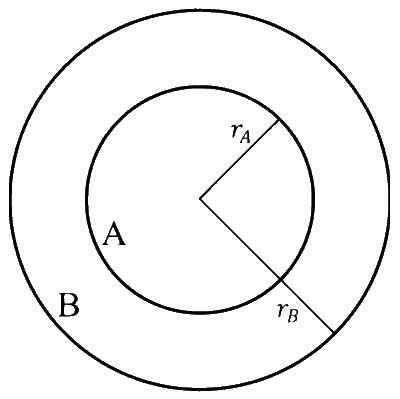
Which of the following statement(s) is(are) correct?
If $r_{B}=\sqrt{\frac{3}{2}}$, then the electric field is zero everywhere outside $B$.
If $r_{B}=\frac{3}{2}$, then the electric potential just outside $B$ is $\frac{k}{\epsilon_{0}}$.
If $r_{B}=2$, then the total charge of the configuration is $15 \pi k$.
If $r_{B}=\frac{5}{2}$, then the magnitude of the electric field just outside $B$ is $\frac{13 \pi k}{\epsilon_{0}}$.
Explanation
$\begin{aligned} Q_{\text {Total }} & =\int_0^{r_A} k r\left(4 \pi r^2\right) d r+\int_{r_A}^{r_B} \frac{2 k}{r}\left(4 \pi r^2\right) d r \\\\ & =\frac{4 \pi k}{4} r_A^4+\frac{8 \pi k}{2}\left(r_B^2-r_A^2\right) \\\\ & =\pi k+4 \pi k\left(r_B^2-r_A^2\right)\end{aligned}$
(A) If $\mathrm{r}_{\mathrm{B}} =\sqrt{\frac{3}{2}}, \ r_A=1 $
$ \mathrm{Q}_{\text {total }} =\pi k r_A^4+4 \pi k\left(\frac{3}{2}-r_A^2\right) $
$ =\pi k+4 \pi k\left(\frac{3}{2}-1\right) $
$ =3 \pi k$
(B) If $ r_B=\frac{3}{2} \& r_A=1 $
$ \mathrm{Q}_{\text {total }}=\pi k r_A^4+4 \pi k\left(\frac{9}{4}-1\right) $
$ =6 \pi k $$ \mathrm{~V}=\frac{1}{4 \pi \varepsilon_0}\left(\frac{6 \pi k}{r_B}\right)=\frac{k}{\varepsilon_0} $
$ \text { Hence, } \quad \mathrm{V}=\frac{k}{\varepsilon_0} $
(C) If $ r_B =2 $
$ \mathrm{Q}_{\text {total }} =13 \pi K$
(D) If $ r_B =5 / 2 $
$ Q_{\text {total }} =22 \pi k $
$ E =\frac{1}{4 \pi \varepsilon_0} \frac{(22 \pi k)}{25} \times 4 $
$$ \Rightarrow $$ $E =\frac{22 k}{25 \varepsilon_0}$
Comments (0)


