JEE Advance - Physics (2022 - Paper 2 Online - No. 5)
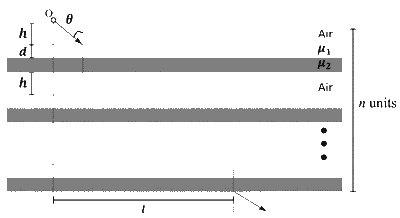
Consider a configuration of $n$ identical units, each consisting of three layers. The first layer is a column of air of height $h=\frac{1}{3} \mathrm{~cm}$, and the second and third layers are of equal thickness $d=$ $\frac{\sqrt{3}-1}{2} \mathrm{~cm}$, and refractive indices $\mu_{1}=\sqrt{\frac{3}{2}}$ and $\mu_{2}=\sqrt{3}$, respectively. A light source 0 is placed on the top of the first unit, as shown in the figure. A ray of light from 0 is incident on the second layer of the first unit at an angle of $\theta=60^{\circ}$ to the normal. For a specific value of $n$, the ray of light emerges from the bottom of the configuration at a distance $l=\frac{8}{\sqrt{3}} \mathrm{~cm}$, as shown in the figure. The value of $n$ is ________.
Answer
4
Explanation
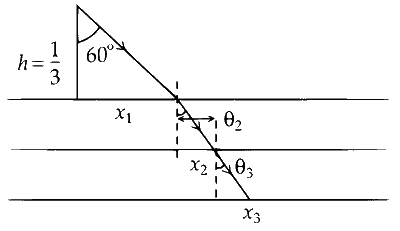
$$ \begin{aligned} &x_1 =\frac{1}{3} \times \tan 60 \\\\ & =\frac{1}{\sqrt{3}} \mathrm{~cm} \end{aligned} $$
By Snell's law
$$ \begin{aligned} &1 \times \sin 60 =\frac{\sqrt{3}}{\sqrt{2}} \sin \theta_2 \\\\ & \Rightarrow \theta_2 =45^ \mathrm{o} \\\\ &\therefore x_2 =d \end{aligned} $$
Again, by applying Snell's law
$$ \begin{aligned} &\sqrt{\frac{3}{2} \times \frac{1}{\sqrt{2}}} =\sqrt{3} \times \sin \theta_3 \\\\ &\Rightarrow \theta_2 =30^{\circ} \\\\ & \therefore x_3 =\frac{d}{\sqrt{3}} \end{aligned} $$
Also
$$ \begin{aligned} & x_1+x_2+x_3 =\frac{1}{\sqrt{3}}+d+\frac{d}{\sqrt{3}} \\\\ & =\frac{1}{\sqrt{3}}+\left(\frac{\sqrt{3}-1}{2}\right)+\frac{\sqrt{3}-1}{2 \sqrt{3}} \\\\ & =\frac{2+(3-\sqrt{3})+\sqrt{3}-1}{2 \sqrt{3}} \\\\ & =\frac{4}{2 \sqrt{3}} \\\\ & x_1+x_2+x_3 =\frac{2}{\sqrt{3}} \mathrm{~cm} \\\\ & \text {And,}~~ \eta =\frac{l}{x_1+x_2+x_3} \\\\ &\eta =\frac{8 / \sqrt{3}}{2 / \sqrt{3}}=4 \\\\ &\eta =4 \end{aligned} $$
Comments (0)


