JEE Advance - Physics (2022 - Paper 2 Online - No. 18)
Which one of the following options represents the magnetic field $\vec{B}$ at $\mathrm{O}$ due to the current flowing in the given wire segments lying on the $x y$ plane?
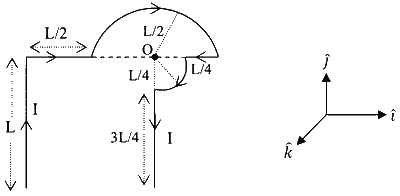
Explanation
$=\frac{\mu_0 I}{4\left(\frac{L}{2}\right)}(-\hat{k})+\frac{\mu_0 I}{8 \times\left(\frac{L}{4}\right)}(-\hat{k})+\frac{\mu_0 I}{4 \pi \times L}\left(\frac{1}{\sqrt{2}}\right)(-\hat{k})$
$=\left(\frac{\mu_0 I}{2 L}+\frac{\mu_0 I}{2 L}+\frac{\mu_0 I}{4 \sqrt{2} \pi L}\right)(-\hat{k})$
$=\frac{\mu_0 I}{L}\left(1+\frac{1}{4 \sqrt{2} \pi}\right)(-\hat{k})$
Things you should know to solve this problem :
(1) Magnetic Field Due to Straight Current Carrying Wire :
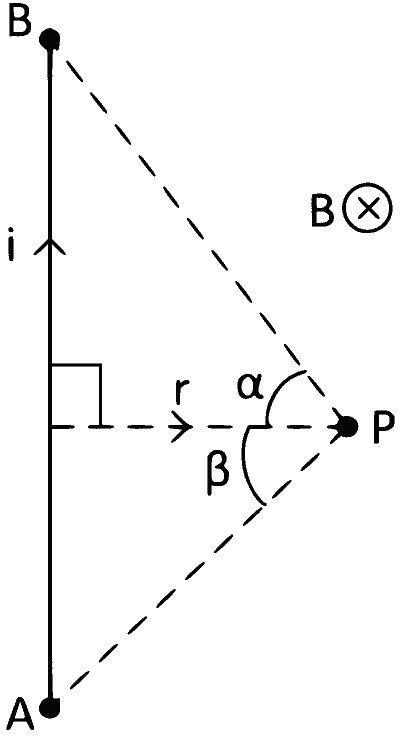
$$B = {{{\mu _0}i} \over {4\pi r}}\left( {\sin \alpha + \sin \beta } \right)$$
Direction of B :
Note :-
On the axis of the wire magnetic field = 0.
Case 1 :
Infinite long wire (Very Long wire) :
$$\alpha ,\beta \to 90^\circ $$
$$\therefore$$ $$B = {{{\mu _0}i} \over {4\pi r}}(\sin 90^\circ + \sin 90^\circ )$$
$$ = {{{\mu _0}i} \over {4\pi r}}(1 + 1)$$
$$ = {{{\mu _0}i} \over {2\pi r}}$$
Graph :
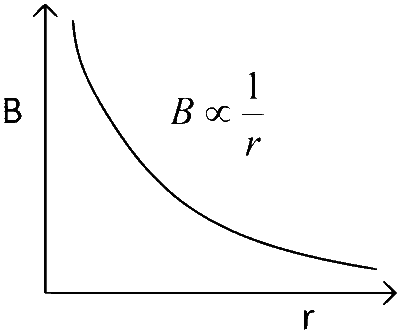
Case 2 :
One end is at infinite and other end is in front.
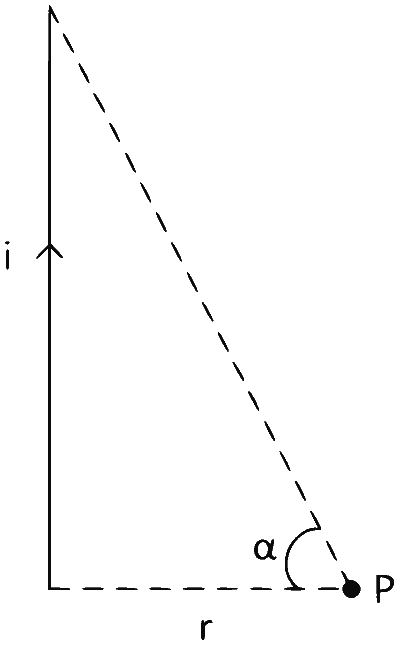
Here $$\alpha=90^\circ$$ and $$\beta=0^\circ$$
$$B = {{{\mu _0}i} \over {4\pi r}}(\sin 90^\circ + \sin 0^\circ )$$
$$ = {{{\mu _0}i} \over {4\pi r}}$$
Case 3 :
When drawn perpendicular from P don't lie on the wire
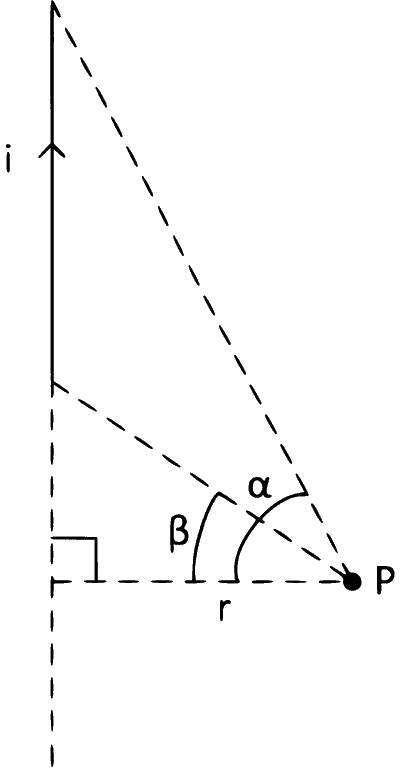
Here, magnetic field at point P is,
$$B = {{{\mu _0}i} \over {4\pi r}}(\sin\alpha-\sin\beta)$$
(2) Magnetic Field Due to Half Loop or Semicircle :
Half loop means $${1 \over 2}$$ turn. So, N = $${1 \over 2}$$.
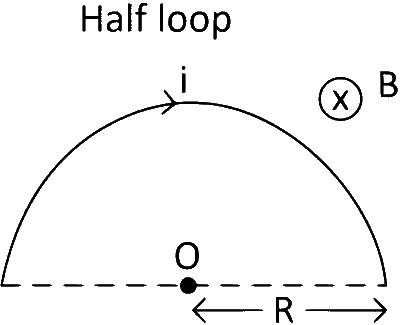
Magnetic field at centre O,
$$\therefore$$ B at centre $$ = {{{\mu _0} \times {1 \over 2} \times i} \over {2R}} = {{{\mu _0}i} \over {4R}}$$
Here,
Here, $$N=\frac{1}{2}$$
i = Amount of current flowing through loop
R = Radius of half loop
Direction of B found by right hand thumb rule. Curl your right hand's finger in the direction of current then thumb gives direction of magnetic field on axis as well as entire plane.
(3) Magnetic Field Due to Quarter Loop :
Quarter loop means $${1 \over 4}$$ turn. So, N = $${1 \over 4 }$$.
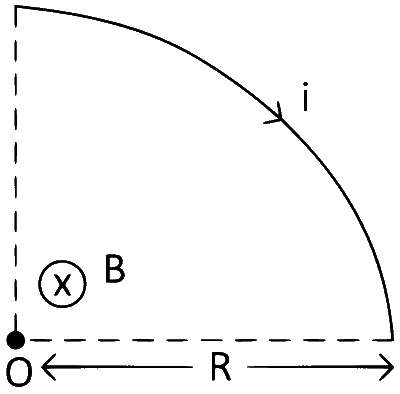
Magnetic field at O,
$$\therefore$$ B at centre $$ = {{{\mu _0} \times {1 \over 4} \times i} \over {2R}} = {{{\mu _0}i} \over {8R}}$$
Here,
Here, $$N=\frac{1}{4}$$
i = Amount of current flowing through loop
R = Radius of quarter loop
Direction of B found by right hand thumb rule. Curl your right hand's finger in the direction of current then thumb gives direction of magnetic field on axis as well as entire plane.
Comments (0)


