JEE Advance - Physics (2022 - Paper 2 Online - No. 14)
In the given $P-V$ diagram, a monoatomic gas $\left(\gamma=\frac{5}{3}\right)$ is first compressed adiabatically from state $A$ to state $B$. Then it expands isothermally from state $B$ to state $C$. [Given: $\left(\frac{1}{3}\right)^{0.6} \simeq 0.5, \ln 2 \simeq 0.7$ ].
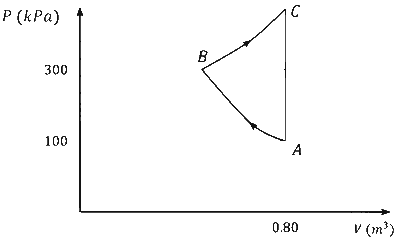
Which of the following statement(s) is(are) correct?
The magnitude of the total work done in the process $A \rightarrow B \rightarrow C$ is $144 \mathrm{~kJ}$.
The magnitude of the work done in the process $B \rightarrow C$ is $84 \mathrm{~kJ}$.
The magnitude of the work done in the process $A \rightarrow B$ is $60 \mathrm{~kJ}$.
The magnitude of the work done in the process $C \rightarrow A$ is zero.
Explanation
For adiabatic process $(\mathrm{A} \rightarrow \mathrm{B})$
$$ \begin{aligned} & \mathrm{P}_{\mathrm{A}} \mathrm{V}_{\mathrm{A}}^\gamma=\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}}^\gamma \\\\ & 10^5 \times(0.8)^{\frac{5}{3}}=3 \times 10^5\left(\mathrm{~V}_{\mathrm{B}}\right)^{\frac{5}{3}} \\\\ & \Rightarrow \mathrm{V}_{\mathrm{B}}=0.8 \times\left(\frac{1}{3}\right)^{0.6}=0.4 \end{aligned} $$
Work done in process $\mathrm{A} \rightarrow \mathrm{B}$
$$ \begin{aligned} & \mathrm{W}_{\mathrm{AB}}=\frac{\mathrm{P}_{\mathrm{A}} \mathrm{V}_{\mathrm{A}}-\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}}}{\gamma-1} \\\\ & \Rightarrow \mathrm{W}_{\mathrm{AB}}=\frac{10^5 \times 0.8-3 \times 10^5 \times 0.4}{\frac{5}{3}-1} \\\\ & \Rightarrow \mathrm{W}_{\mathrm{AB}}=-60 \mathrm{~kJ}=\Rightarrow\left|\mathrm{W}_{\mathrm{AB}}\right|=60 \mathrm{~kJ} \end{aligned} $$
Work done in process $\mathrm{B} \rightarrow \mathrm{C}$ (Isothermal process)
$$ \begin{aligned} & \mathrm{W}_{\mathrm{BC}}=\mathrm{nRT} \ell \mathrm{n} \frac{\mathrm{V}_{\mathrm{C}}}{\mathrm{V}_{\mathrm{B}}}=\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}} \ell \mathrm{n} \frac{\mathrm{V}_{\mathrm{C}}}{\mathrm{V}_{\mathrm{B}}} \\\\ & \Rightarrow \mathrm{W}_{\mathrm{BC}}=3 \times 10^5 \times 0.4 \ell \mathrm{n} \frac{0.8}{0.4} \\\\ & \Rightarrow \mathrm{W}_{\mathrm{BC}}=84 \mathrm{~kJ} \end{aligned} $$
Work done in process $\mathrm{C} \rightarrow \mathrm{A}$
$$ \mathrm{W}_{\mathrm{CA}}=\mathrm{P} \Delta \mathrm{V}=0 \quad(\because \Delta \mathrm{V}=0) $$
So total work done in the process $\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C}$
$$ \begin{aligned} & \mathrm{W}_{\mathrm{ABC}}=\mathrm{W}_{\mathrm{AB}}+\mathrm{W}_{\mathrm{BC}}+\mathrm{W}_{\mathrm{CA}}=-60+84+0 \\\\ & \mathrm{~W}_{\mathrm{ABC}}=24 \mathrm{~kJ} \end{aligned} $$
So correct options are (B,C,D)
$$ \begin{aligned} & \mathrm{P}_{\mathrm{A}} \mathrm{V}_{\mathrm{A}}^\gamma=\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}}^\gamma \\\\ & 10^5 \times(0.8)^{\frac{5}{3}}=3 \times 10^5\left(\mathrm{~V}_{\mathrm{B}}\right)^{\frac{5}{3}} \\\\ & \Rightarrow \mathrm{V}_{\mathrm{B}}=0.8 \times\left(\frac{1}{3}\right)^{0.6}=0.4 \end{aligned} $$
Work done in process $\mathrm{A} \rightarrow \mathrm{B}$
$$ \begin{aligned} & \mathrm{W}_{\mathrm{AB}}=\frac{\mathrm{P}_{\mathrm{A}} \mathrm{V}_{\mathrm{A}}-\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}}}{\gamma-1} \\\\ & \Rightarrow \mathrm{W}_{\mathrm{AB}}=\frac{10^5 \times 0.8-3 \times 10^5 \times 0.4}{\frac{5}{3}-1} \\\\ & \Rightarrow \mathrm{W}_{\mathrm{AB}}=-60 \mathrm{~kJ}=\Rightarrow\left|\mathrm{W}_{\mathrm{AB}}\right|=60 \mathrm{~kJ} \end{aligned} $$
Work done in process $\mathrm{B} \rightarrow \mathrm{C}$ (Isothermal process)
$$ \begin{aligned} & \mathrm{W}_{\mathrm{BC}}=\mathrm{nRT} \ell \mathrm{n} \frac{\mathrm{V}_{\mathrm{C}}}{\mathrm{V}_{\mathrm{B}}}=\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}} \ell \mathrm{n} \frac{\mathrm{V}_{\mathrm{C}}}{\mathrm{V}_{\mathrm{B}}} \\\\ & \Rightarrow \mathrm{W}_{\mathrm{BC}}=3 \times 10^5 \times 0.4 \ell \mathrm{n} \frac{0.8}{0.4} \\\\ & \Rightarrow \mathrm{W}_{\mathrm{BC}}=84 \mathrm{~kJ} \end{aligned} $$
Work done in process $\mathrm{C} \rightarrow \mathrm{A}$
$$ \mathrm{W}_{\mathrm{CA}}=\mathrm{P} \Delta \mathrm{V}=0 \quad(\because \Delta \mathrm{V}=0) $$
So total work done in the process $\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C}$
$$ \begin{aligned} & \mathrm{W}_{\mathrm{ABC}}=\mathrm{W}_{\mathrm{AB}}+\mathrm{W}_{\mathrm{BC}}+\mathrm{W}_{\mathrm{CA}}=-60+84+0 \\\\ & \mathrm{~W}_{\mathrm{ABC}}=24 \mathrm{~kJ} \end{aligned} $$
So correct options are (B,C,D)
Comments (0)


