Sign In

JEE Advance - Physics (2022 - Paper 2 Online - No. 13)

A double slit setup is shown in the figure. One of the slits is in medium 2 of refractive index $n_{2}$. The other slit is at the interface of this medium with another medium 1 of refractive index $n_{1}\left(\neq n_{2}\right)$. The line joining the slits is perpendicular to the interface and the distance between the slits is $d$. The slit widths are much smaller than $d$. A monochromatic parallel beam of light is incident on the slits from medium 1. A detector is placed in medium 2 at a large distance from the slits, and at an angle $\theta$ from the line joining them, so that $\theta$ equals the angle of refraction of the beam. Consider two approximately parallel rays from the slits received by the detector.

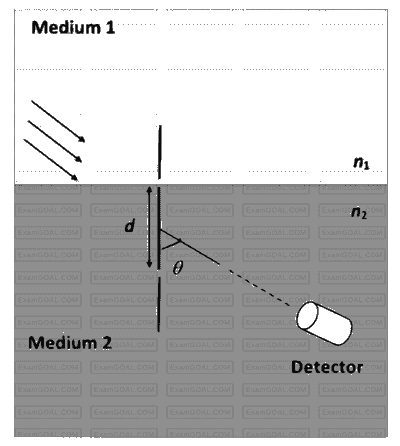
JEE Advanced 2022 Paper 2 Online Physics - Wave Optics Question 7 English

Which of the following statement(s) is(are) correct?

The phase difference between the two rays is independent of $d$.
The two rays interfere constructively at the detector.
The phase difference between the two rays depends on $n_{1}$ but is independent of $n_{2}$.
The phase difference between the two rays vanishes only for certain values of $d$ and the angle of incidence of the beam, with $\theta$ being the corresponding angle of refraction.

Explanation

JEE Advanced 2022 Paper 2 Online Physics - Wave Optics Question 7 English Explanation

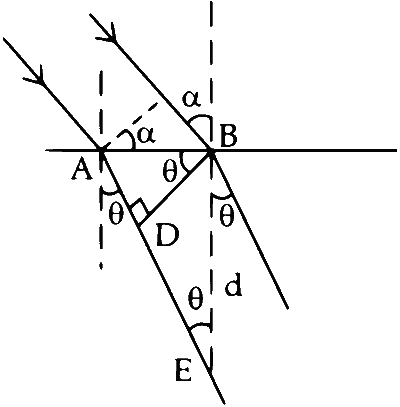
$ \tan \theta =\frac{\mathrm{AB}}{d}$

And, $ \mathrm{AB} =d \tan \theta $ ........ (i)

$ \mathrm{BC} =\mathrm{AB} \sin \alpha $

$ =d \tan \theta \sin \alpha $

$ \mathrm{AD} =\mathrm{AB} \sin \theta $

Path difference in vacuum

$$ \begin{aligned} \Delta x & =n_1 \mathrm{BC}-n_2 \mathrm{AD} \\\\ \Delta x & =n_1(\mathrm{AB}) \sin \alpha-n_2(\mathrm{AB} \sin \theta) \end{aligned} $$

Hence, $\mathrm{AB}\left(n_1 \sin \alpha-n_2 \sin \theta\right)=0$

Comments (0)

Advertisement