JEE Advance - Physics (2022 - Paper 2 Online - No. 10)
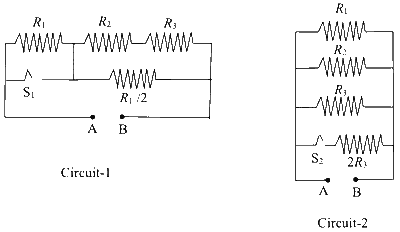
In Circuit-1 and Circuit- 2 shown in the figures, $R_{1}=1 \,\Omega, R_{2}=2 \,\Omega$ and $R_{3}=3 \,\Omega$.
$P_{1}$ and $P_{2}$ are the power dissipations in Circuit-1 and Circuit-2 when the switches $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ are in open conditions, respectively.
$Q_{1}$ and $Q_{2}$ are the power dissipations in Circuit-1 and Circuit-2 when the switches $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ are in closed conditions, respectively.
Which of the following statement(s) is(are) correct?
$P_{1}$ and $P_{2}$ are the power dissipations in Circuit-1 and Circuit-2 when the switches $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ are in open conditions, respectively.
$Q_{1}$ and $Q_{2}$ are the power dissipations in Circuit-1 and Circuit-2 when the switches $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ are in closed conditions, respectively.

Which of the following statement(s) is(are) correct?
When a voltage source of $6 V$ is connected across $\mathrm{A}$ and $\mathrm{B}$ in both circuits, $P_{1} < P_{2}$.
When a constant current source of $2 \mathrm{Amp}$ is connected across A and B in both circuits, $P_{1}>P_{2}$.
When a voltage source of $6 V$ is connected across $\mathrm{A}$ and $\mathrm{B}$ in Circuit-1, $Q_{1}>P_{1}$.
When a constant current source of $2 \mathrm{Amp}$ is connected across A and $\mathrm{B}$ in both circuits, $Q_{2} < Q_{1}$.
Explanation
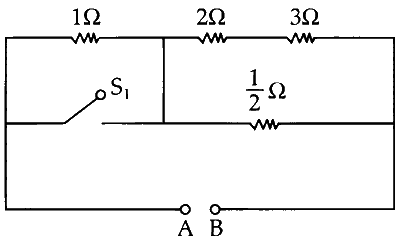
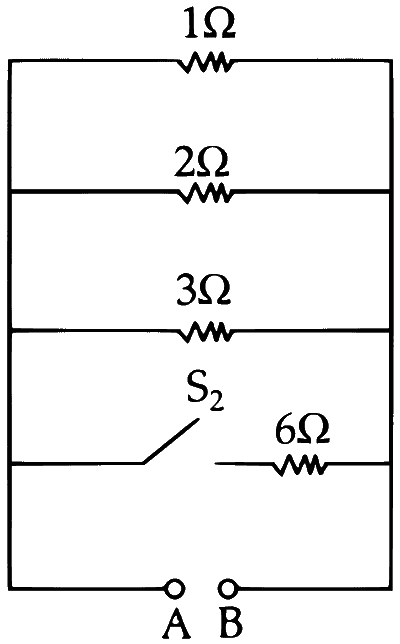
Case 1 : When $\mathrm{S}_1$ and $\mathrm{S}_2$ are open
$ \left(R_{e q}\right)_1=1+\frac{5 \times \frac{1}{2}}{5+\frac{1}{2}}=1+\frac{5}{11}=\frac{16}{11} $
$ P_1=\frac{V^2}{(R_{e q})_1}=\frac{(6)^2}{16} \times 11=\frac{36 \times 11}{16}=24.75 \mathrm{~W} $
$ \left(R_{e q}\right)_2=\frac{6}{11} \Omega $
$ P_2=\frac{V^2}{(R_{e q})_2}=\frac{(6)^2}{6} \times 11=\frac{36 \times 11}{6}=66 \mathrm{~W} $
$ P_2>P_1 $
Option (A) is correct.
Case 2 : If I = $2 \mathrm{~A}$ source is used in both circuits, then
$ P_1=i^2\left(R_{e q}\right)_1=(2)^2 \times \frac{16}{11}=\frac{64}{11}=5.818 \mathrm{~W} $
$ P_2=i^2\left(R_{e q}\right)_2=(2)^2 \times \frac{6}{11}=\frac{24}{11}=2.1818 \mathrm{~W} $
$ P_1>P_2 $
Option (B) is correct.
Case 3 : For $Q_1$
$$ \begin{aligned} & R_{e q}=\frac{5}{11} \Omega \\\\ & Q_1=\frac{V^2}{R_{e q}}=\frac{(6)^2}{\frac{5}{11}}=\frac{36 \times 11}{5}=79.2 \mathrm{~W} \\\\ & P_1=24.75 \mathrm{~W} \\\\ & Q_1>P_1 \end{aligned} $$
Option (C) is correct.
Case 4 : For option (D)
$$ \begin{aligned} & Q_1=i^2 R_{e q}=(2)^2 \times \frac{5}{11}=\frac{20}{11}=1.81 \mathrm{~W} \\\\ & Q_2=i^2 R_{e q}=(2)^2 \times \frac{1}{2}=\frac{4}{2}=2 \mathrm{~W} \\\\ & Q_2>Q_1 \end{aligned} $$
Option (D) is incorrect.
Comments (0)


