Sign In

JEE Advance - Physics (2022 - Paper 1 Online - No. 9)

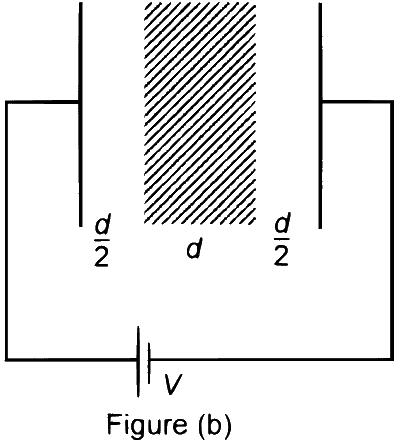
A medium having dielectric constant $K>1$ fills the space between the plates of a parallel plate capacitor. The plates have large area, and the distance between them is $d$. The capacitor is connected to a battery of voltage $V$, as shown in Figure (a). Now, both the plates are moved by a distance of $\frac{d}{2}$ from their original positions, as shown in Figure (b).

JEE Advanced 2022 Paper 1 Online Physics - Capacitor Question 4 English

In the process of going from the configuration depicted in Figure (a) to that in Figure (b), which of the following statement(s) is(are) correct?

The electric field inside the dielectric material is reduced by a factor of $2 K$.
The capacitance is decreased by a factor of $\frac{1}{K+1}$.
The voltage between the capacitor plates is increased by a factor of $(K+1)$.
The work done in the process DOES NOT depend on the presence of the dielectric material.

Explanation

JEE Advanced 2022 Paper 1 Online Physics - Capacitor Question 4 English Explanation 1

$C_a=\frac{K \varepsilon_0 A}{d}$

$$ \therefore $$ $q_a=\frac{K \varepsilon_0 A}{d} V$

$ E_a =\frac{q_a}{K A \varepsilon_0}$

$=\frac{K \varepsilon_0 A V}{d K \varepsilon_0 A} $

$ =\frac{V}{d}$

JEE Advanced 2022 Paper 1 Online Physics - Capacitor Question 4 English Explanation 2

$\begin{aligned} C_b & =\frac{\varepsilon_0 A}{d+\left(\frac{d}{K}\right)} \\\\ & =\frac{\varepsilon_0 A K}{d(K+1)}\end{aligned}$

$q_b=\frac{\varepsilon_0 A K V}{d(K+1)}$

$\left(E_b\right)_{\text {dielectric }} $

$=\frac{E_{\text {air }}}{K} $

$=\frac{q_b}{K A \varepsilon_0} $

$=\frac{\varepsilon_0 A K V}{d(K+1)\left(K A \varepsilon_0\right)}$

$ =\frac{V}{d(K+1)}$

$\begin{aligned} &\therefore\text { Capacitance decrease by a factor of } \frac{1}{K+1} \\\\ & \text { Work done in the process }=U_f-U_i \\\\ &=\frac{1}{2}\left(C_f-C_i\right) V^2 \\\\ &=\frac{1}{2}\left(\frac{\varepsilon_0 A K}{d(K+1)}-\frac{K \varepsilon_0 A}{d}\right) V^2 \\\\ &=\frac{1}{2} V^2 \frac{\varepsilon_0 A K}{d}\left(\frac{1}{K+1}-1\right) \\\\ &=\frac{1}{2} \frac{\varepsilon_0 A K V^2}{d} \frac{1-K-1}{K+1} \\\\ &=\frac{1}{2} \frac{\varepsilon_0 A V^2}{d}\left(\frac{-K^2}{K+1}\right)\end{aligned}$

Comments (0)

Advertisement