JEE Advance - Physics (2022 - Paper 1 Online - No. 6)
A solid sphere of mass $1 \mathrm{~kg}$ and radius $1 \mathrm{~m}$ rolls without slipping on a fixed inclined plane with an angle of inclination $\theta=30^{\circ}$ from the horizontal. Two forces of magnitude $1 \mathrm{~N}$ each, parallel to the incline, act on the sphere, both at distance $r=0.5 \mathrm{~m}$ from the center of the sphere, as shown in the figure. The acceleration of the sphere down the plane is _________ $m \,s^{-2} .\left(\right.$ Take $g=10\, m s^{-2}$)

Answer
2.86
Explanation
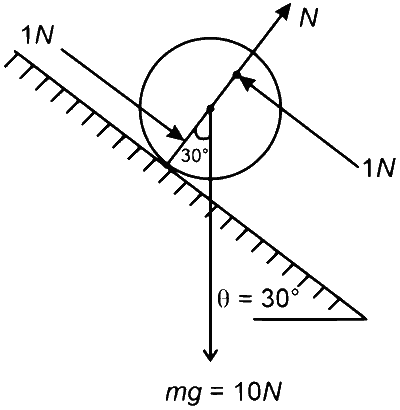
Taking torque about contact point.
$\vec{\tau}=m g R \sin 30^{\otimes}+1 \times 1^{\odot}$
taking $\otimes$ is positive
$$ \begin{aligned} & 5-1=\frac{7}{5} m R^2 \alpha \\\\ & \Rightarrow \quad \alpha=\frac{20}{7} \mathrm{rad} / \mathrm{s}^2 \end{aligned} $$
So, $a_{\mathrm{cm}}=\alpha R=\frac{20}{7} \mathrm{~m} / \mathrm{s}^2$
$$ a_{\mathrm{cm}}=2.86 \mathrm{~m} / \mathrm{s}^2 $$
Comments (0)


