JEE Advance - Physics (2022 - Paper 1 Online - No. 16)

List I describes four systems, each with two particles $A$ and $B$ in relative motion as shown in figures. List II gives possible magnitudes of their relative velocities (in $m s^{-1}$ ) at time $t=\frac{\pi}{3} s$.

List-I	List-II
(I) $A$ and $B$ are moving on a horizontal circle of radius $1 \mathrm{~m}$ with uniform angular speed $\omega=1 \mathrm{rad} \mathrm{s}^{-1}$. The initial angular positions of $A$ and $B$ at time $t=0$ are $\theta=0$ and $\theta=\frac{\pi}{2}$, respectively.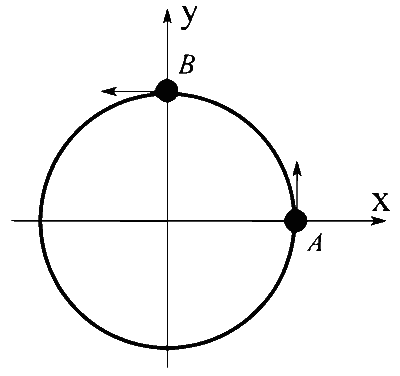	(P) $\frac{\sqrt{3}+1}{2}$
(II) Projectiles $A$ and $B$ are fired (in the same vertical plane) at $t=0$ and $t=0.1 \mathrm{~s}$ respectively, with the same speed $v=\frac{5 \pi}{\sqrt{2}} \mathrm{~m} \mathrm{~s}^{-1}$ and at $45^{\circ}$ from the horizontal plane. The initial separation between $A$ and $B$ is large enough so that they do not collide. $\left(g=10 \mathrm{~ms}^{-2}\right)$.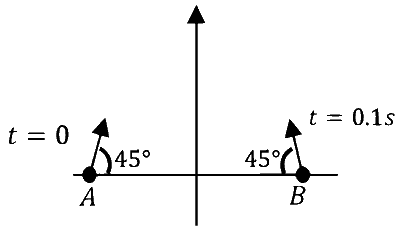	(Q) $\frac{\sqrt{3}-1}{\sqrt{2}}$
(III) Two harmonic oscillators $A$ and $B$ moving in the $x$ direction according to $x_{A}=x_{0} \sin \frac{t}{t_{0}}$ and $x_{B}=x_{0} \sin \left(\frac{t}{t_{0}}+\frac{\pi}{2}\right)$ respectively, starting from $t=0$. Take $x_{0}=1 \mathrm{~m}, t_{0}=1 \mathrm{~s}$.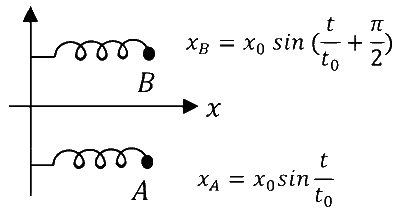	(R) $\sqrt{10}$
(IV) Particle $A$ is rotating in a horizontal circular path of radius $1 \mathrm{~m}$ on the $x y$ plane, with constant angular speed $\omega=1 \mathrm{rad} \mathrm{s}^{-1}$. Particle $B$ is moving up at a constant speed $3 \mathrm{~m} \mathrm{~s}^{-1}$ in the vertical direction as shown in the figure. (Ignore gravity.)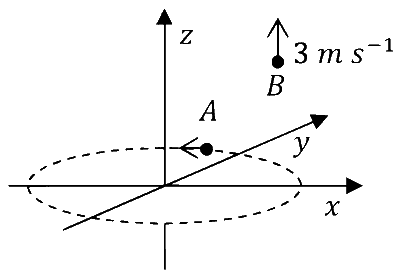	(S) $\sqrt{2}$
	(T) $\sqrt{25\pi^{2}+1}$

Which one of the following options is correct?

I $\rightarrow$ R, II $\rightarrow$ T, III $\rightarrow$ P, IV $\rightarrow$ S

I $\rightarrow$ S, II $\rightarrow$ P, III $\rightarrow$ Q, IV $\rightarrow$ R

I $\rightarrow$ S, II $\rightarrow$ T, III $\rightarrow$ P, IV $\rightarrow$ R

I $\rightarrow$ T, II $\rightarrow$ P, III $\rightarrow$ R, IV $\rightarrow$ S

Explanation

(I) 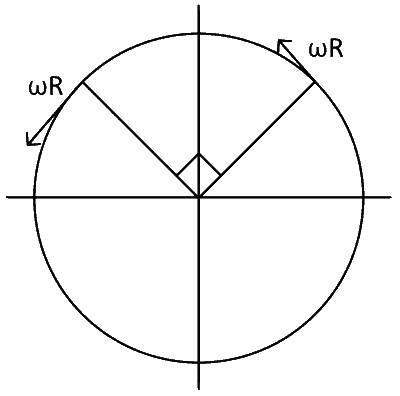JEE Advanced 2022 Paper 1 Online Physics - Rotational Motion Question 19 English Explanation

$${v_{net}} = \sqrt 2 \omega R = \sqrt 2 $$

I $$\to$$ S

(II) $${v_A}(t = 0.13) = {{5\pi } \over {\sqrt 2 }}\cos 45\widehat i + \left[ {{{5\pi } \over {\sqrt 2 }} \times {1 \over {\sqrt 2 }} - g \times 0.1} \right]\widehat j$$

$$ = {{5\pi } \over 2}\widehat i + \left( {{{5\pi } \over 2} - 1} \right)\widehat j$$

$${v_B}(t = 0.1\,\sec ) = {{ - 5\pi } \over 2}\widehat i + \left( {{{5\pi } \over 2}} \right)\widehat j$$

After $$t = 0.1$$, relative velocities should not change.

$${v_{rel}}(t = 0.1\,\sec ) = \left| {5\pi \widehat i - \widehat j} \right|$$

$$ = \sqrt {25{\pi ^2} + 1} $$

II $$\to$$ T

(III) $$x = {x_A} - {x_B}$$

$$ = {x_0}\sin t - {x_0}\sin \left( {t + {\pi \over 2}} \right)$$

$$ = \sqrt 2 {x_0}\sin \left( {t - {\pi \over 4}} \right)$$

$${v_{rel}} = {{dx} \over {dt}} = \sqrt 2 {x_0}\cos \left( {t - {\pi \over 4}} \right)$$

$$ = \sqrt 2 \cos \left( {{\pi \over 3} - {\pi \over 4}} \right)$$

$$ = \sqrt 2 \times {{\sqrt 3 + 1} \over {2\sqrt 2 }} = {{\sqrt 3 + 1} \over 2}$$

III $$\to$$ P

(IV) $${v_{rel}} = \sqrt {{3^2} + {1^2}} = \sqrt {10} $$

IV $$\to$$ R

JEE Advance - Physics (2022 - Paper 1 Online - No. 16)

Explanation

Comments (0)