JEE Advance - Physics (2022 - Paper 1 Online - No. 15)
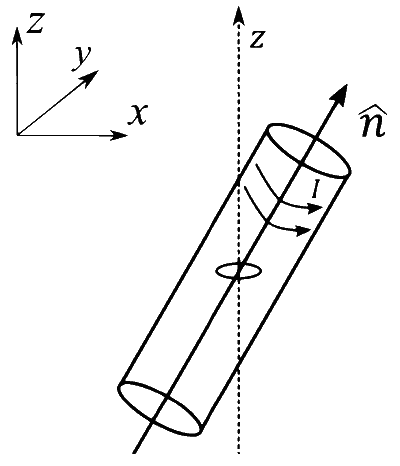
A small circular loop of area $A$ and resistance $R$ is fixed on a horizontal $x y$-plane with the center of the loop always on the axis $\hat{n}$ of a long solenoid. The solenoid has $m$ turns per unit length and carries current $I$ counterclockwise as shown in the figure. The magnetic field due to the solenoid is in $\hat{n}$ direction. List-I gives time dependences of $\hat{n}$ in terms of a constant angular frequency $\omega$. List-II gives the torques experienced by the circular loop at time $t=\frac{\pi}{6 \omega}$. Let $\alpha=\frac{A^{2} \mu_{0}^{2} m^{2} I^{2} \omega}{2 R}$.
| List-I | List-II |
|---|---|
| (I) $\frac{1}{\sqrt{2}}(\sin \omega t \hat{\jmath}+\cos \omega t \hat{k})$ | (P) 0 |
| (II) $\frac{1}{\sqrt{2}}(\sin \omega t \hat{\imath}+\cos \omega t \hat{\jmath})$ | (Q) $-\frac{\alpha}{4} \hat{\imath}$ |
| (III) $\frac{1}{\sqrt{2}}(\sin \omega t \hat{\imath}+\cos \omega t \hat{k})$ | (R) $\frac{3 \alpha}{4} \hat{\imath}$ |
| (IV) $\frac{1}{\sqrt{2}}(\cos \omega t \hat{\jmath}+\sin \omega t \hat{k})$ | (S) $\frac{\alpha}{4} \hat{\jmath}$ |
| (T) $-\frac{3 \alpha}{4} \hat{\imath}$ |
Which one of the following options is correct?
Explanation
I. $$\phi = B\,A\,\widehat k\,.\,\widehat n$$
$$\phi = {{BA} \over {\sqrt 2 }}\cos (\omega t)$$
$$\varepsilon = {{BA\omega } \over {\sqrt 2 }}\sin (\omega t)$$
$$i = {{BA\omega } \over {\sqrt 2 R}}\sin (\omega t)$$
$$\overrightarrow m = iA\,\widehat k = {{B{A^2}\omega } \over {\sqrt 2 R}}\sin (\omega t)\widehat k$$
$$\overrightarrow \tau = \overrightarrow m \times \overrightarrow B = {{{B^2}{A^2}\omega } \over {\sqrt 2 R}}\sin (\omega t)(\widehat k \times \widehat n)$$
$$ = - {{{B^2}{A^2}\omega } \over {2R}}\left[ {\widehat i} \right]{\sin ^2}(\omega t)$$
$$\tau = - {{{B^2}{A^2}\omega } \over {2R}}\left[ {{{\sin }^2}\left( {{\pi \over 6}} \right)} \right] = {{ - \alpha } \over 4}\widehat i$$
(I) $$\to$$ Q.
II. $$\phi = O$$
(II) $$\to$$ P.
III. $$\phi = {{BA\omega } \over {\sqrt 2 }}\cos (\omega t)$$
$$i = {{BA\omega } \over {\sqrt 2 R}}\sin (\omega t)$$
$$\overrightarrow m = {{B{A^2}\omega } \over {\sqrt 2 R}}\sin (\omega t)\widehat k$$
$$\overrightarrow \tau = \overrightarrow m \times \overrightarrow B = {{{B^2}{A^2}\omega } \over {\sqrt 2 \times \sqrt 2 R}}\sin \omega t(\widehat k \times (\sin \omega t\widehat i + \cos \omega t\widehat k))$$
$$\tau = {{{B^2}{A^2}\omega \sin (\omega t)} \over {2R}}\sin (\omega t)\widehat j$$
$$ = {{{B^2}{A^2}\omega } \over {2R}}{\sin ^2}(\omega t)\widehat j$$
$$ = {\alpha \over 4}\widehat j$$
(III) $$\to$$ S.
IV. $$\phi = {{BA} \over {\sqrt 2 }}\sin (\omega t)$$
$$i = - {{BA\omega } \over {\sqrt 2 R}}\cos (\omega t)$$
$$\overrightarrow m = - {{B{A^2}\omega } \over {\sqrt 2 R}}\cos \omega t(\widehat k)$$
$$\overrightarrow \tau = \overrightarrow m \times \overrightarrow B = - {{{B^2}{A^2}\omega } \over {2R}}(\widehat k \times \widehat j){\cos ^2}(\omega t)$$
$$\tau = + {{{B^2}{A^2}\omega } \over {2R}}(\widehat i)\,.\,{\cos ^2}\left( {{\pi \over 6}} \right)$$
$$ = + {3 \over 4}\alpha \widehat i$$
(IV) $$\to$$ R.
Comments (0)


