JEE Advance - Physics (2021 - Paper 2 Online - No. 3)
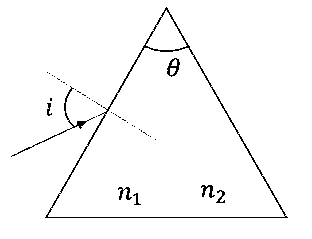
For a prism of prism angle $$\theta$$ = 60$$^\circ$$, the refractive indices of the left half and the right half are, respectively, n1 and n2 (n2 $$\ge$$ n1) as shown in the figure. The angle of incidence i is chosen such that the incident light rays will have minimum deviation if n1 = n2 = n = 1.5. For the case of unequal refractive indices, n1 = n and n2 = n + $$\Delta$$n (where $$\Delta$$n << n), the angle of emergence e = i + $$\Delta$$e. Which of the following statement(s) is(are) correct?

The value of $$\Delta$$e (in radians) is greater than that of $$\Delta$$n
$$\Delta$$e is proportional to $$\Delta$$n
$$\Delta$$e lies between 2.0 and 3.0 milliradians, if $$\Delta$$n = 2.8 $$\times$$ 10$$-$$3
$$\Delta$$e lies between1.0 and 1.6 milliradians, if $$\Delta$$n = 2.8 $$\times$$ 10$$-$$3
Explanation
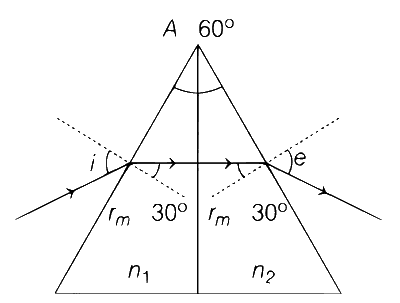
$${n_1} = {n_2} = n = {3 \over 2}$$ for minimum deviation.
$${r_m} = {A \over 2} = {{60} \over 2} = 30^\circ $$ and $$i = e = \theta $$
$$n = {{\sin \left( {{{{\delta _{\min }} + A} \over 2}} \right)} \over {\sin \left( {{A \over 2}} \right)}} $$
$$\Rightarrow {3 \over 2} = {{\sin \theta } \over {\sin \left( {{{60} \over 2}} \right)}}$$
$$ \Rightarrow \sin \theta = {3 \over 4} \Rightarrow \cos \theta = {{\sqrt 7 } \over 4}$$
If $${n_1} = n = {3 \over 2}$$ and $${n_2} = n + \Delta n$$
$$e = \theta + \Delta \theta $$
$$(1)\sin \theta = n\sin 30^\circ $$
$$(n + \Delta n)\sin 30^\circ = (1)\sin (\theta + \Delta \theta )$$
Solving $${1 \over 2}(\Delta n) = \sin (\theta + \Delta \theta ) - \sin \theta $$
$${{\Delta n} \over 2} = {{\sin (\theta + \Delta \theta ) - sin\theta } \over {\Delta \theta }} \times \Delta \theta $$
$${{d(\sin \theta )} \over {d\theta }} = \cos \theta $$
$${{\Delta n} \over 2} = (\cos \theta )(\Delta \theta ) \Rightarrow {{\Delta n} \over 2} = {{\sqrt 7 } \over 4}(\Delta \theta )$$
$$ \Rightarrow {{\Delta n} \over {\Delta \theta }} = {{\sqrt 7 } \over 2} = {{2.64} \over 2}$$
$${{\Delta n} \over {\Delta \theta }} = 1.34 > 1$$
$$\Rightarrow$$ $$\Delta$$n > $$\Delta$$$$\theta$$, so option (a) is incorrect.
$$\Delta n = (1.34)\Delta \theta $$
$$ \Rightarrow \Delta \theta \propto \Delta n \Rightarrow $$ option (b) is correct.
$${{\Delta n} \over {\Delta \theta }} = {{\sqrt 7 } \over 2} \Rightarrow {{2.8 \times {{10}^{ - 3}}} \over {\Delta \theta }} = {{\sqrt 7 } \over 2}$$
$$\Delta \theta = {{5.6 \times {{10}^{ - 3}}} \over {\sqrt 7 }} = \sqrt 7 \times 0.8 \times {10^{ - 3}}$$
$$\Delta \theta = (2.64 \times 0.8) \times {10^{ - 3}} = 2.11 \times {10^{ - 3}}$$ rad
So, option (c) is correct.
Comments (0)


