Sign In

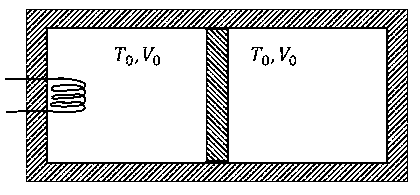
JEE Advance - Physics (2021 - Paper 2 Online - No. 16)

A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, CV = 2R. Here, R is the gas constant. Initially, each side has a volume V0 and temperature T0. The left side has an electric heater, which is turned on at very low power to transfer heat Q to the gas on the left side. As a result the partition moves slowly towards the right reducing the right side volume to V0/2. Consequently, the gas temperatures on the left and the right sides become TL and TR, respectively. Ignore the changes in the temperatures of the cylinder, heater and the partition.

A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, CV = 2R. Here, R is the gas constant. Initially, each side has a volume V0 and temperature T0. The left side has an electric heater, which is turned on at very low power to transfer heat Q to the gas on the left side. As a result the partition moves slowly towards the right reducing the right side volume to V0/2. Consequently, the gas temperatures on the left and the right sides become TL and TR, respectively. Ignore the changes in the temperatures of the cylinder, heater and the partition.

A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, CV = 2R. Here, R is the gas constant. Initially, each side has a volume V0 and temperature T0. The left side has an electric heater, which is turned on at very low power to transfer heat Q to the gas on the left side. As a result the partition moves slowly towards the right reducing the right side volume to V0/2. Consequently, the gas temperatures on the left and the right sides become TL and TR, respectively. Ignore the changes in the temperatures of the cylinder, heater and the partition.

The value of $${Q \over {R{T_0}}}$$ is
$$4(2\sqrt 2 + 1)$$
$$4(2\sqrt 2 - 1)$$
$$(5\sqrt 2 + 1)$$
$$(5\sqrt 2 - 1)$$

Explanation

$$Q = \Delta U = \Delta {U_1} + \Delta {U_2}$$

$$\Delta {U_2} = 1 \times 2R \times (\sqrt 2 {T_0} - {T_0}) + 2R{T_0}(\sqrt 2 - 1)$$

For $$\Delta$$U2 : Using mole conservation of left side.

$${{{p_0}{V_0}} \over {R{T_0}}} = {{2\sqrt 2 {p_0}{{3{V_0}} \over 2}} \over {R{T_L}}} \Rightarrow {T_L} = 3\sqrt 2 {T_0}$$

$$\Delta {U_1} = 1 \times 2R \times (3\sqrt 2 {T_0} - {T_0}) = 2R{T_0}(3\sqrt 2 - 1)$$

$$Q = 2R{T_0}(\sqrt 2 - 1) + 2R{T_0}(3\sqrt 2 - 1) = 2R{T_0}(4\sqrt 2 - 2)$$

$${{\Delta Q} \over {R{T_0}}} = 2(4\sqrt 2 - 1)$$

Comments (0)

Advertisement