JEE Advance - Physics (2021 - Paper 2 Online - No. 13)
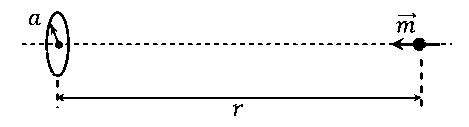
A special metal S conducts electricity without any resistance. A closed wire loop, made of S, does not allow any change in flux through itself by inducing a suitable current to generate a compensating flux. The induced current in the loop cannot decay due to its zero resistance. This current gives rise to a magnetic moment which in turn repels the source of magnetic field or flux. Consider such a loop, of radius a, with its center at the origin. A magnetic dipole of moment m is brought along the axis of this loop from infinity to a point at distance r (>> a) from the center of the loop with its north pole always facing the loop, as shown in the figure below.
The magnitude of magnetic field of a dipole m, at a point on its axis at distance r, is $${{{\mu _0}} \over {2\pi }}{m \over {{r^3}}}$$, where $$\mu$$0 is the permeability of free space. The magnitude of the force between two magnetic dipoles with moments, m1 and m2, separated by a distance r on the common axis, with their north poles facing each other, is $${{k{m_1}{m_2}} \over {{r^4}}}$$, where k is a constant of appropriate dimensions. The direction of this force is along the line joining the two dipoles.
The magnitude of magnetic field of a dipole m, at a point on its axis at distance r, is $${{{\mu _0}} \over {2\pi }}{m \over {{r^3}}}$$, where $$\mu$$0 is the permeability of free space. The magnitude of the force between two magnetic dipoles with moments, m1 and m2, separated by a distance r on the common axis, with their north poles facing each other, is $${{k{m_1}{m_2}} \over {{r^4}}}$$, where k is a constant of appropriate dimensions. The direction of this force is along the line joining the two dipoles.

A special metal S conducts electricity without any resistance. A closed wire loop, made of S, does not allow any change in flux through itself by inducing a suitable current to generate a compensating flux. The induced current in the loop cannot decay due to its zero resistance. This current gives rise to a magnetic moment which in turn repels the source of magnetic field or flux. Consider such a loop, of radius a, with its center at the origin. A magnetic dipole of moment m is brought along the axis of this loop from infinity to a point at distance r (>> a) from the center of the loop with its north pole always facing the loop, as shown in the figure below.
The magnitude of magnetic field of a dipole m, at a point on its axis at distance r, is $${{{\mu _0}} \over {2\pi }}{m \over {{r^3}}}$$, where $$\mu$$0 is the permeability of free space. The magnitude of the force between two magnetic dipoles with moments, m1 and m2, separated by a distance r on the common axis, with their north poles facing each other, is $${{k{m_1}{m_2}} \over {{r^4}}}$$, where k is a constant of appropriate dimensions. The direction of this force is along the line joining the two dipoles.

The magnitude of magnetic field of a dipole m, at a point on its axis at distance r, is $${{{\mu _0}} \over {2\pi }}{m \over {{r^3}}}$$, where $$\mu$$0 is the permeability of free space. The magnitude of the force between two magnetic dipoles with moments, m1 and m2, separated by a distance r on the common axis, with their north poles facing each other, is $${{k{m_1}{m_2}} \over {{r^4}}}$$, where k is a constant of appropriate dimensions. The direction of this force is along the line joining the two dipoles.

A special metal S conducts electricity without any resistance. A closed wire loop, made of S, does not allow any change in flux through itself by inducing a suitable current to generate a compensating flux. The induced current in the loop cannot decay due to its zero resistance. This current gives rise to a magnetic moment which in turn repels the source of magnetic field or flux. Consider such a loop, of radius a, with its center at the origin. A magnetic dipole of moment m is brought along the axis of this loop from infinity to a point at distance r (>> a) from the center of the loop with its north pole always facing the loop, as shown in the figure below.
The magnitude of magnetic field of a dipole m, at a point on its axis at distance r, is $${{{\mu _0}} \over {2\pi }}{m \over {{r^3}}}$$, where $$\mu$$0 is the permeability of free space. The magnitude of the force between two magnetic dipoles with moments, m1 and m2, separated by a distance r on the common axis, with their north poles facing each other, is $${{k{m_1}{m_2}} \over {{r^4}}}$$, where k is a constant of appropriate dimensions. The direction of this force is along the line joining the two dipoles.

The magnitude of magnetic field of a dipole m, at a point on its axis at distance r, is $${{{\mu _0}} \over {2\pi }}{m \over {{r^3}}}$$, where $$\mu$$0 is the permeability of free space. The magnitude of the force between two magnetic dipoles with moments, m1 and m2, separated by a distance r on the common axis, with their north poles facing each other, is $${{k{m_1}{m_2}} \over {{r^4}}}$$, where k is a constant of appropriate dimensions. The direction of this force is along the line joining the two dipoles.

When the dipole m is placed at a distance r from the center of the loop (as shown in the figure), the current induced in the loop will be proportional to
m/r3
m2/r2
m/r2
m2/r
Explanation
$$\phi = Li = {{{\mu _0}m} \over {2\pi {r^3}}} \times \pi {a^2}$$
$$ \Rightarrow i = {{{\mu _0}m\pi {a^2}} \over {2\pi {r^3}L}} \Rightarrow i \propto {m \over {{r^3}}}$$
$$ \Rightarrow i = {{{\mu _0}m\pi {a^2}} \over {2\pi {r^3}L}} \Rightarrow i \propto {m \over {{r^3}}}$$
Comments (0)


