JEE Advance - Physics (2021 - Paper 2 Online - No. 1)
One end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point O and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point Q, at a height L above the hinge at point O. A block of weight $$\alpha$$W is attached at the point P of the beam, as shown in the figure (not to scale). The rope can sustain a maximum tension of (2$$\sqrt 2 $$)W. Which of the following statement(s) is(are) correct?


The vertical component of reaction force at O does not depend on $$\alpha$$
The horizontal component of reaction force at O is equal to W for $$\alpha$$ = 0.5
The tension in the rope is 2W for $$\alpha$$ = 0.5
The rope breaks if $$\alpha$$ > 1.5
Explanation
Free body diagram of rod
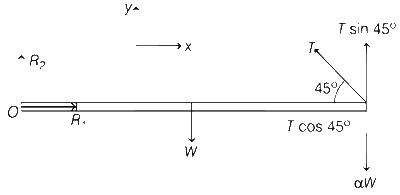
$$\sum {{F _x} = 0} $$
$${R_1} = T\cos 45^\circ $$
$${R_1} = {T \over {\sqrt 2 }}$$ ..... (i)
$$\sum {{F_y} = 0} $$
$${R_2} + T\sin 45^\circ = W + \alpha W$$
$${R_2} + {T \over {\sqrt 2 }} = W(1 + \alpha )$$ ..... (ii)
$$\sum {{\tau _0} = 0} $$
$$W{L \over 2} + \alpha WL = {T \over {\sqrt 2 }}L$$
$$T = \sqrt 2 W\left[ {\alpha + {1 \over 2}} \right]$$ ..... (iii)
From Eqs. (ii) and (iii), we get
$${R_2} + W\left[ {\alpha + {1 \over 2}} \right] = W(1 + \alpha )$$
$${R_2} = {W \over 2}$$
Hence, option (a) is correct.
From Eqs. (i) and (iii), we get
$${R_1} = W\left[ {\alpha + {1 \over 2}} \right]$$
$$\alpha$$ = 0.5, R1 = W
Hence, option (b) is correct.
From Eq. (iii), if $$\alpha$$ = 0.5
$$T = \sqrt 2 W$$
$${T_{\max }} = 2\sqrt 2 W$$
For rope to break,
$$T > 2\sqrt 2 W$$
$$\sqrt 2 W\left[ {\alpha + {1 \over 2}} \right] > 2\sqrt 2 W \Rightarrow \alpha > {3 \over 2}$$
Hence, option (d) is correct.

$$\sum {{F _x} = 0} $$
$${R_1} = T\cos 45^\circ $$
$${R_1} = {T \over {\sqrt 2 }}$$ ..... (i)
$$\sum {{F_y} = 0} $$
$${R_2} + T\sin 45^\circ = W + \alpha W$$
$${R_2} + {T \over {\sqrt 2 }} = W(1 + \alpha )$$ ..... (ii)
$$\sum {{\tau _0} = 0} $$
$$W{L \over 2} + \alpha WL = {T \over {\sqrt 2 }}L$$
$$T = \sqrt 2 W\left[ {\alpha + {1 \over 2}} \right]$$ ..... (iii)
From Eqs. (ii) and (iii), we get
$${R_2} + W\left[ {\alpha + {1 \over 2}} \right] = W(1 + \alpha )$$
$${R_2} = {W \over 2}$$
Hence, option (a) is correct.
From Eqs. (i) and (iii), we get
$${R_1} = W\left[ {\alpha + {1 \over 2}} \right]$$
$$\alpha$$ = 0.5, R1 = W
Hence, option (b) is correct.
From Eq. (iii), if $$\alpha$$ = 0.5
$$T = \sqrt 2 W$$
$${T_{\max }} = 2\sqrt 2 W$$
For rope to break,
$$T > 2\sqrt 2 W$$
$$\sqrt 2 W\left[ {\alpha + {1 \over 2}} \right] > 2\sqrt 2 W \Rightarrow \alpha > {3 \over 2}$$
Hence, option (d) is correct.
Comments (0)


