JEE Advance - Physics (2021 - Paper 1 Online - No. 3)
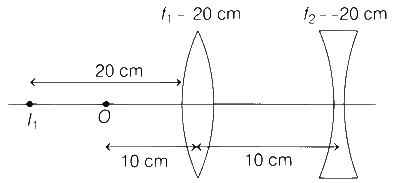
An extended object is placed at point O, 10 cm in front of a convex lens L1 and a concave lens L2 is placed 10 cm behind it, as shown in the figure. The radii of curvature of all the curved surfaces in both the lenses ae 20 cm. The refractive index of both the lenses is 1.5. The total magnification of this lens system is


0.4
0.8
1.3
1.6
Explanation
Focal length of convex lens f1,
Therefore $${1 \over {{f_1}}} = (\mu - 1)\left[ {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right] = (1.5 - 1)\left[ {{1 \over {20}} - \left( {{1 \over { - 20}}} \right)} \right]$$
$$\Rightarrow$$ f1 = + 20 cm
Focal length of concave lens f2,
$$\therefore$$ $${1 \over {{f_2}}} = (\mu - 1)\left[ {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right]$$
$${1 \over {{f_2}}} = (1.5 - 1)\left[ { - {1 \over {20}} - {1 \over {20}}} \right] = {1 \over { - 20}}$$
$$\Rightarrow$$ f2 = $$-$$ 20 cm
For lens 1
$${1 \over v} - {1 \over u} = {1 \over f}$$
$$\Rightarrow$$ v = $$-$$ 20 cm
$${m_1} = {v \over u} = {{ - 20} \over { - 10}} = 2$$
For lens 2
u = $$-$$ 30n cm, f = $$-$$ 20 cm,
$${1 \over v} - {1 \over u} = {1 \over f}$$
v = $$-$$ 12 cm
$${m_2} = {v \over u} = {{ - 12} \over { - 30}} = {2 \over 5}$$
Net magnification,
$$m = {m_1}{m_2} = 2 \times {2 \over 5} = {4 \over 5} = 0.8$$
Therefore $${1 \over {{f_1}}} = (\mu - 1)\left[ {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right] = (1.5 - 1)\left[ {{1 \over {20}} - \left( {{1 \over { - 20}}} \right)} \right]$$
$$\Rightarrow$$ f1 = + 20 cm
Focal length of concave lens f2,
$$\therefore$$ $${1 \over {{f_2}}} = (\mu - 1)\left[ {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right]$$
$${1 \over {{f_2}}} = (1.5 - 1)\left[ { - {1 \over {20}} - {1 \over {20}}} \right] = {1 \over { - 20}}$$
$$\Rightarrow$$ f2 = $$-$$ 20 cm
For lens 1

$${1 \over v} - {1 \over u} = {1 \over f}$$
$$\Rightarrow$$ v = $$-$$ 20 cm
$${m_1} = {v \over u} = {{ - 20} \over { - 10}} = 2$$
For lens 2
u = $$-$$ 30n cm, f = $$-$$ 20 cm,
$${1 \over v} - {1 \over u} = {1 \over f}$$
v = $$-$$ 12 cm
$${m_2} = {v \over u} = {{ - 12} \over { - 30}} = {2 \over 5}$$
Net magnification,
$$m = {m_1}{m_2} = 2 \times {2 \over 5} = {4 \over 5} = 0.8$$
Comments (0)


