JEE Advance - Physics (2021 - Paper 1 Online - No. 16)
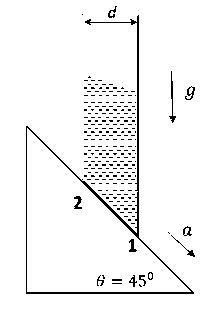
A cylindrical tube, with its base as shown in the figure, is filled with water. It is moving down with a constant acceleration a along a fixed inclined plane with angle $$\theta$$ = 45$$^\circ$$. P1 and P2 are pressures at points 1 and 2, respectively, located at the base of the tube. Let $$\beta$$ = (P1 $$-$$ P2)/($$\rho$$gd), where $$\rho$$ is density of water, d is the inner diameter of the tube and g is the acceleration due to gravity. Which of the following statement(s) is(are) correct?

$$\beta$$ = 0 when a = g/$$\sqrt 2 $$
$$\beta$$ > 0 when a = g/$$\sqrt 2 $$
$$\beta = {{\sqrt 2 - 1} \over {\sqrt 2 }}$$ when a = g/2
$$\beta = {1 \over {\sqrt 2 }}$$ when a = g/2
Explanation
$$({p_1} - {p_2})ds = \rho dsd\sqrt 2 (g\sin 45^\circ - a)$$
$$({p_1} - {p_2})ds = \rho d(g - a\sqrt 2 )$$
$$\beta = {{({p_1} - {p_2})} \over {\rho gd}} = \left( {1 - {{a\sqrt 2 } \over g}} \right)$$
When $$a = {g \over {\sqrt 2 }},\beta = 0$$
When $$a = {g \over 2},\beta = \left( {{{\sqrt 2 - 1} \over {\sqrt 2 }}} \right)$$
$$({p_1} - {p_2})ds = \rho d(g - a\sqrt 2 )$$
$$\beta = {{({p_1} - {p_2})} \over {\rho gd}} = \left( {1 - {{a\sqrt 2 } \over g}} \right)$$
When $$a = {g \over {\sqrt 2 }},\beta = 0$$
When $$a = {g \over 2},\beta = \left( {{{\sqrt 2 - 1} \over {\sqrt 2 }}} \right)$$
Comments (0)


