JEE Advance - Physics (2021 - Paper 1 Online - No. 15)
A long straight wire carries a current, I = 2 ampere. A semi-circular conducting rod is placed beside it on two conducting parallel rails of negligible resistance. Both the rails are parallel to the wire. The wire, the rod and the rails lie in the same horizontal plane, as shown in the figure. Two ends of the semi-circular rod are at the distances 1 cm and 4 cm from the wire. At time t = 0, the rod starts moving on the rails with a speed v = 3.0 m/s (see the figure).
A resistor R = 1.4 $$\Omega$$ and a capacitor C0 = 5.0$$\mu$$F are connected in series between the rails. At time t = 0, C0 is uncharged. Which of the following statement(s) is(are) correct? [$$\mu$$0 = 4$$\pi$$ $$\times$$ 10$$-$$7 SI units. Take ln 2 = 0.7]
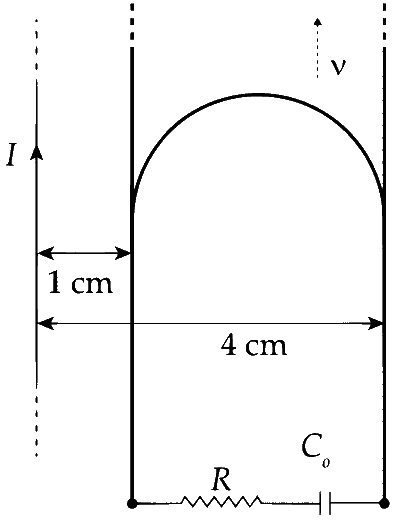
A resistor R = 1.4 $$\Omega$$ and a capacitor C0 = 5.0$$\mu$$F are connected in series between the rails. At time t = 0, C0 is uncharged. Which of the following statement(s) is(are) correct? [$$\mu$$0 = 4$$\pi$$ $$\times$$ 10$$-$$7 SI units. Take ln 2 = 0.7]

Maximum current through R is 1.2 $$\times$$ 10$$-$$6 ampere
Maximum current through R is 3.8 $$\times$$ 10$$-$$6 ampere
Maximum charge on capacitor C0 is 8.4 $$\times$$ 10$$-$$12 coulomb
Maximum charge on capacitor C0 is 2.4 $$\times$$ 10$$-$$12 coulomb
Explanation
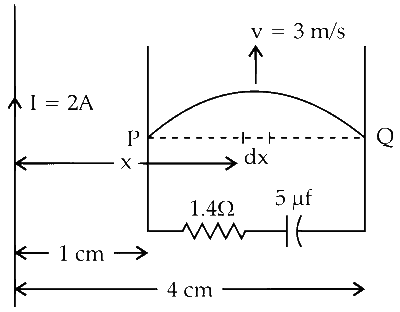
Let a small element of length $d x$ be chosen at a distance $x$ from the wire. Induced emf de across it is given by
$$ \begin{aligned} d \mathrm{E} & =\mathrm{B} v(d x) \\\\ & =\frac{\mu_0 \mathrm{I}}{2 \pi x} v(d x) \\\\ \mathrm{E}_{\mathrm{PQ}} & =\frac{\mu_0 \mathrm{I} v}{2 \pi} \int_1^4 \frac{d x}{x} \\\\ \mathrm{E}_{\mathrm{PQ}} & =\frac{\mu_0 \mathrm{I} v}{2 \pi} \ln 4=\frac{\mu_0 \mathrm{I} v}{2 \pi} \times 2 \ln 2 \end{aligned} $$
On substituting all the values in above, we get
$$ \begin{aligned} \mathrm{E}_{\mathrm{PQ}} & =2 \times 10^{-7} \times 2 \times 3 \times 2 \times 0.7 \\\\ & =16.8 \times 10^{-7} \mathrm{~V} \end{aligned} $$
At $t=0, \mathrm{C}$ acts as a short. So, maximum current flows through $R$.
$$ \begin{aligned} i_{\max } & =\frac{\mathrm{E}_{\mathrm{PQ}}}{\mathrm{R}}=\frac{16.8 \times 10^{-7}}{1.4} \\\\ & =12 \times 10^{-7} \mathrm{~A} \\\\ & =1.2 \times 10^{-6} \mathrm{~A} \end{aligned} $$
At $t \rightarrow \infty, C$ acts as on open. So,
$$ \begin{aligned} q_{\max } & =\mathrm{CE}_{\mathrm{PQ}}=5 \times 10^{-6} \times 16.8 \times 10^{-7} \mathrm{C} \\\\ & =84 \times 10^{-13} \mathrm{C} \\\\ & =8.4 \times 10^{-12} \mathrm{C} \end{aligned} $$
Comments (0)


