JEE Advance - Physics (2021 - Paper 1 Online - No. 12)
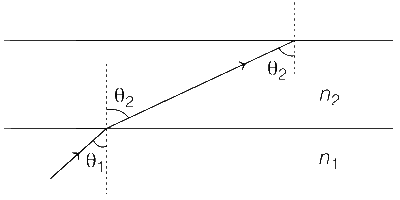
A wide slab consisting of two media of refractive indices n1 and n2 is placed in air as shown in the figure. A ray of light is incident from medium n1 to n2 at an angle $$\theta$$, where sin$$\theta$$ is slightly larger than 1/n1. Take refractive index of air as 1. Which of the following statement(s) is(are) correct?
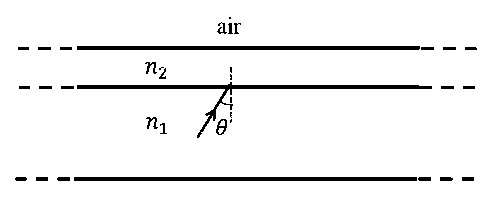

The light ray enters air if n2 = n1
The light ray is finally reflected back into the medium of refractive index n1 if n2 < n1
The light ray is finally reflected back into the medium of refractive index n1 if n2 > n1
The light ray is reflected back into the medium of refractive index n1 if n2 = 1
Explanation
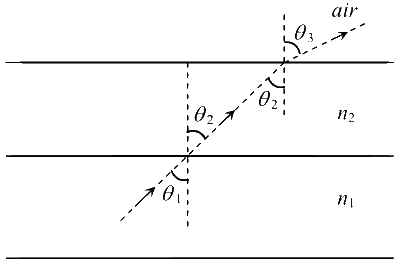
$$\sin \theta > {1 \over {{n_1}}}$$ (Given)
i.e., $$\sin {\theta _1} > {1 \over {{n_1}}}$$
$${n_1}\sin {\theta _1} = {n_2}\sin {\theta _2}$$
$$\sin {\theta _2} = {{{n_1}\sin {\theta _1}} \over {{n_2}}}$$
if $${n_1} = {n_2}$$ then $${\theta _2} = {\theta _1}$$
$${n_2}\sin {\theta _2} = (1)\sin {\theta _3}$$
$$\sin {\theta _3} = {n_2}\sin {\theta _2}$$
$$\sin {\theta _3} = {n_1}\sin {\theta _1}$$
$$\sin {\theta _1} = {{\sin {\theta _3}} \over {{n_1}}} > {1 \over {{n_1}}}$$
$$\sin {\theta _3} > 1$$
$${\theta _3} > 90^\circ $$
This means ray cannot enter air.
For $${n_1} > {n_2};\sin {\theta _1} = {{{n_2}} \over {{n_1}}}\sin {\theta _2} > {1 \over {{n_1}}}$$
$$\sin {\theta _2} > {1 \over {{n_2}}}$$
For surface 2 - air interface
$${n_2}\sin {\theta _2} = \sin {\theta _3}$$
$$\sin {\theta _2} = {{\sin {\theta _3}} \over {{n_2}}} > {1 \over {{n_2}}}$$
$${\theta _2} > 90^\circ $$
It means ray is reflected back in medium-2
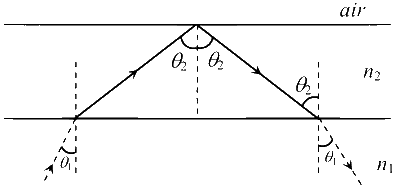
For surface 1 and surface 2 interface
$${n_2}\sin {\theta _2} = {n_1}\sin {\theta _1}$$
$$\sin {\theta _{2C}} = {{{n_1}} \over {{n_2}}}$$
$${\theta _{2C}}$$ : critical angle
For ray to enter medium - 1
$${\theta _2} < {\theta _{2C}}$$
$$\sin {\theta _2} < \sin 2{\theta _C}$$
$${{{n_1}} \over {{n_2}}}\sin {\theta _1} < {{{n_1}} \over {{n_2}}}$$
$$\sin {\theta _1} < 1$$
$${\theta _1} < 90^\circ $$, which is true.
Hence, ray enters medium - 1
For $${n_2} > {n_1}$$
$${{{n_2}} \over {{n_1}}}\sin {\theta _2} > {{{n_2}} \over {{n_1}}}$$
$$\sin {\theta _2} > {1 \over {{n_2}}}$$
For surface 2 - air interface
$${n_2}\sin {\theta _2} = \sin {\theta _3}$$
$$\sin {\theta _2} = {{\sin {\theta _3}} \over {{n_2}}} > {1 \over {{n_2}}}$$
$${\theta _2} > 90$$
It means ray reflected back in medium - 2
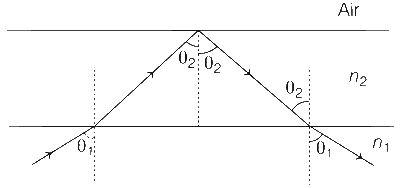
$${n_2}\sin {\theta _2} = {n_1}\sin {\theta _1}$$
$$\sin {\theta _1} = {{{n_2}} \over {{n_1}}}\sin {\theta _2}$$
$$\sin {\theta _{2C}} = {{{n_1}} \over {{n_2}}};{\theta _{2C}}$$ $$\to$$ critical angle
For ray to enter medium - 1
$${\theta _2} < {\theta _{2C}}$$
$$\sin {\theta _2} < \sin {\theta _{2C}}$$
$${{{n_1}} \over {{n_2}}}\sin {\theta _1} < {{{n_1}} \over {{n_2}}}$$
$$\sin {\theta _1} < 1$$
$${\theta _1} = 90^\circ $$, which is true.
Hence, ray enters medium - 1
Let, n2 = 1
$${n_1}\sin {\theta _1} = {n_2}\sin {\theta _2} \Rightarrow {n_2} = 1$$
$${n_1}\sin {\theta _1} = \sin {\theta _2}$$
$$\sin {\theta _1} = {{\sin {\theta _2}} \over {{n_1}}} > {1 \over {{n_1}}}$$
$$\sin {\theta _2} > 1 \Rightarrow {\theta _2} = 90^\circ $$
$$\therefore$$ Ray is reflected back in medium.
Comments (0)


