JEE Advance - Physics (2021 - Paper 1 Online - No. 11)
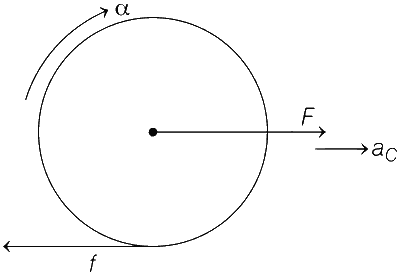
A horizontal force F is applied at the center of mass of a cylindrical object of mass m and radius R, perpendicular to its axis as shown in the figure. The coefficient of friction between the object and the ground is $$\mu$$. The center of mass of the object has an acceleration a. The acceleration due to gravity is g. Given that the object rolls without slipping, which of the following statement(s) is(are) correct?


For the same F, the value of a does not depend on whether the cylinder is solid or hollow
For a solid cylinder, the maximum possible value of a is 2$$\mu$$g
The magnitude of the frictional force on the object due to the ground is always $$\mu$$mg
For a thin-walled hollow cylinder, $$a = {F \over {2m}}$$
Explanation
F $$-$$ f = mac
fR = IC$$\alpha$$
aC $$-$$ $$\alpha$$R = 0
$$F - {I_C}{\alpha \over R} = m{a_c}$$
$${a_C} = {F \over {{{{I_C}} \over {{R^2}}} + m}}$$
$$f = {{{I_C}\alpha } \over R} = {{{I_C}} \over {{R^2}}},{a_C} = {{{I_C}} \over {{R^2}}}{F \over {\left[ {{{{I_C}} \over {{R^2}}} + m} \right]}}$$
$$f = {F \over {\left( {m + {{{I_C}} \over {{R^2}}}} \right)}}$$
Thin walled hollow cylinder,
IC = mR2
$${a_C} = {F \over {2m}}$$
$$fR = {I_C}\alpha = {{{I_C}{a_C}} \over R}$$
$$f = {{{I_C}{a_C}} \over {{R^2}}} \le \mu mg$$
$${a_C} \le {{\mu mg{R^2}} \over {{I_C}}}$$
For solid cylinder, $${I_C} = {{m{R^2}} \over 2}$$
$${a_C} \le 2\mu g$$
$${({a_C})_{\max }} = 2\mu g$$
Comments (0)


