JEE Advance - Physics (2021 - Paper 1 Online - No. 10)
Two point charges $$-$$Q and +Q/$$\sqrt 3 $$ are placed in the xy-plane at the origin (0, 0) and a point (2, 0), respectively, as shown in the figure. This results in an equipotential circle of radius R and potential V = 0 in the xy-plane with its center at (b, 0). All lengths are measured in meters.

The value of b is __________ meter.

The value of b is __________ meter.
Answer
3.00
Explanation
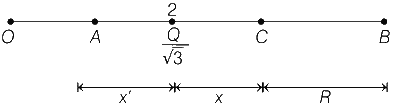
V at B is zero if
$${{kQ} \over {(2 + R + x)}} = {{{{kQ} \over {\sqrt 3 }}} \over {x + R}}$$ ($$\because$$ $$k = {1 \over {4\pi {\varepsilon _0}}}$$)
$$\sqrt 3 (x + R) = 2 + R + x$$
$$(\sqrt 3 - 1)x + (\sqrt 3 - 1)R = 2$$ .....(i)
V at A is zero if
$${{kQ} \over {2 - x'}} = {{{{kQ} \over {\sqrt 3 }}} \over {x'}}$$
$$\sqrt 3 x' = 2 - x'$$
$$x' = {2 \over {\sqrt 3 + 1}}$$
$$x' + x = R$$
$${2 \over {\sqrt 3 + 1}} + x = R$$
$$2 + (\sqrt 3 + 1)x = (\sqrt 3 + 1)R$$
$$x = {{(\sqrt 3 + 1)R - 2} \over {\sqrt 3 + 1}}$$
$$(\sqrt 3 + 1)R - (\sqrt 3 + 1)x = 2$$ .....(ii)
Using Eqs. (i) and (ii), we get
$$R = \sqrt 3 m = 1.73m$$
$$x = {{(\sqrt 3 + 1)\sqrt 3 - 2} \over {\sqrt 3 + 1}} = {{\sqrt 3 + 1} \over {\sqrt 3 + 1}} = 1$$ m
Hence, the centre of circle is having x-coordinate
= b = 2 + x = 3.00 m.
Comments (0)


