JEE Advance - Physics (2020 - Paper 2 Offline - No. 9)
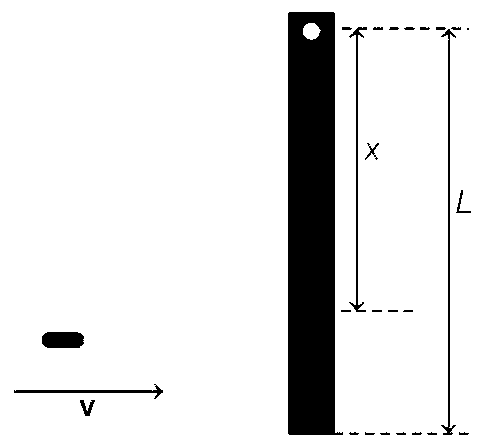
A rod of mass m and length L, pivoted at one of its ends, is hanging vertically. A bullet of the same mass moving at speed v strikes the rod horizontally at a distance x from its pivoted end and gets embedded in it. The combined system now rotates with angular speed $$\omega$$ about the pivot. The maximum angular speed $$\omega$$M is achieved for x = xM. Then

$$\omega = {{3vx} \over {{L^2} + 3{x^2}}}$$
$$\omega = {{12vx} \over {{L^2} + 12{x^2}}}$$
$${x_M} = {L \over {\sqrt 3 }}$$
$${\omega _M} = {v \over {2L}}\sqrt 3 $$
Explanation
According to conservation of angular momentum about suspension point,
$$mvx = \left( {{{m{L^2}} \over 3} + m{x^2}} \right)\omega $$
$$vx = \left( {{{{L^2}} \over 3} + {x^2}} \right)\omega \Rightarrow \omega = {{3vx} \over {{L^2} + 3{x^2}}}$$
For maximum,
$${{d\omega } \over {dx}} = 0 \Rightarrow x = {L \over {\sqrt 3 }} \Rightarrow \omega = {{\sqrt 3 v} \over {2L}}$$
$$mvx = \left( {{{m{L^2}} \over 3} + m{x^2}} \right)\omega $$
$$vx = \left( {{{{L^2}} \over 3} + {x^2}} \right)\omega \Rightarrow \omega = {{3vx} \over {{L^2} + 3{x^2}}}$$
For maximum,
$${{d\omega } \over {dx}} = 0 \Rightarrow x = {L \over {\sqrt 3 }} \Rightarrow \omega = {{\sqrt 3 v} \over {2L}}$$
Comments (0)


