JEE Advance - Physics (2020 - Paper 2 Offline - No. 8)
A student skates up a ramp that makes an angle 30$$^\circ$$ with the horizontal. He/she starts (as shown in the figure) at the bottom of the ramp with speed v0 and wants to turn around over a semicircular path xyz of radius R during which he/she reaches a maximum height h (at point y) from the ground as shown in the figure. Assume that the energy loss is negligible and the force required for this turn at the highest point is provided by his/her weight only. Then (g is the acceleration due to gravity)
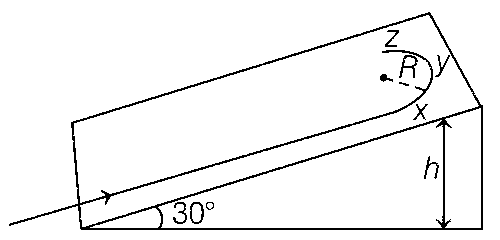

$$v_0^2 - 2gh = {1 \over 2}gR$$
$$v_0^2 - 2gh = {{\sqrt 3 } \over 2}gR$$
the centripetal force required at points x and z is zero
the centripetal force required is maximum at points x and z
Explanation
Apply energy conservation,
$${1 \over 2}mv_0^2 = mgh + {1 \over 2}m{v^2}$$
$${1 \over 2}m{v^2} = {1 \over 2}mv_0^2 - mgh$$ ..... (i)
At top point y, the centripetal force provided by the component of mg,
mg sin$$\theta$$ = centripetal force = $${{m{v^2}} \over R}$$
$${{m{v^2}} \over R} = mg\sin \theta $$
Putting this value in Eq. (i), we get
$${{mgR\sin \theta } \over 2} = {1 \over 2}mv_0^2 - mgh$$
$${{mgR} \over 2}{1 \over 2} = {1 \over 2}mv_0^2 - mgh$$
$${{gR} \over 2} = v_0^2 - 2gh$$
$${1 \over 2}mv_0^2 = mgh + {1 \over 2}m{v^2}$$
$${1 \over 2}m{v^2} = {1 \over 2}mv_0^2 - mgh$$ ..... (i)
At top point y, the centripetal force provided by the component of mg,
mg sin$$\theta$$ = centripetal force = $${{m{v^2}} \over R}$$
$${{m{v^2}} \over R} = mg\sin \theta $$
Putting this value in Eq. (i), we get
$${{mgR\sin \theta } \over 2} = {1 \over 2}mv_0^2 - mgh$$
$${{mgR} \over 2}{1 \over 2} = {1 \over 2}mv_0^2 - mgh$$
$${{gR} \over 2} = v_0^2 - 2gh$$
At point x and a of circular path, the points are at same height but less than h. So the velocity is more than point y.
So required centripetal force = $$\frac{mv^{2}}{r}$$ is more.
Comments (0)


