JEE Advance - Physics (2020 - Paper 2 Offline - No. 7)
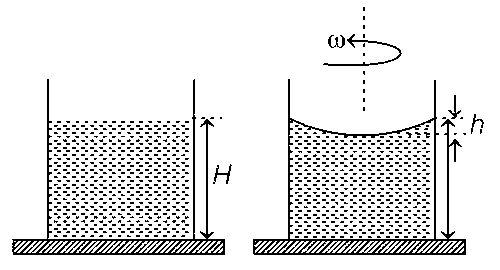
A beaker of radius r is filled with water (refractive index $${4 \over 3}$$) up to a height H as shown in the figure on the left. The beaker is kept on a horizontal table rotating with angular speed $$\omega$$. This makes the water surface curved so that the difference in the height of water level at the center and at the circumference of the beaker is h (h << H, h << r), as shown in the figure on the right. Take this surface to be approximately spherical with a radius of curvature R. Which of the following is/are correct? (g is the acceleration due to gravity)

$$R = {{{h^2} + {r^2}} \over {2h}}$$
$$R = {{3{r^2}} \over {2h}}$$
Apparent depth of the bottom of the beaker is close to $${{3H} \over 2}\left( {1 + {{{\omega ^2}H} \over {2g}}} \right)^{-1}$$
Apparent depth of the bottom of the beaker is close to $${{3H} \over 4}{\left( {1 + {{{\omega ^2}H} \over {4g}}} \right)^{ - 1}}$$
Explanation
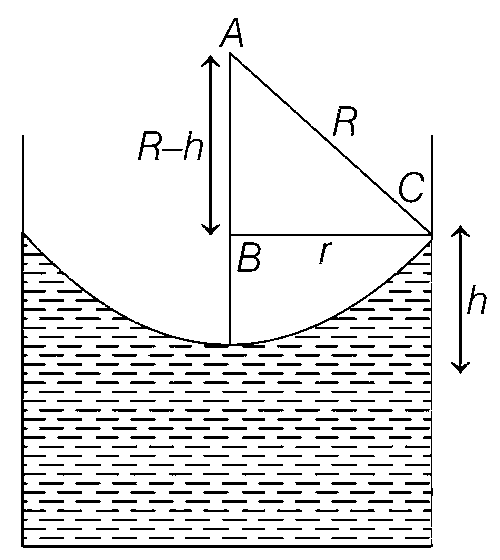
$${(R - h)^2} + {r^2} = {R^2}$$
$${R^2} + {h^2} - 2Rh + {r^2} = {R^2}$$
$${h^2} + {r^2} = 2Rh \Rightarrow {{{h^2} + {r^2}} \over {2h}} = R$$ .....(i)
When r > > > h, then
$$R = {{{r^2}} \over {2h}} \Rightarrow h = {{{\omega ^2}{r^2}} \over {2g}}$$
$$R = {{{r^2}2g} \over {2{\omega ^2}{r^2}}} \Rightarrow R = {g \over {{\omega ^2}}}$$ ..... (ii)
$${{{\mu _1}} \over v} - {{{\mu _2}} \over u} = {{{\mu _1} - {\mu _2}} \over R} $$
$$\Rightarrow {1 \over v} + {4 \over {3u}} = {{1 - {4 \over 3}} \over R}$$
$${1 \over v} = - \left( {{1 \over {3R}} + {4 \over {3(H - h)}}} \right)$$
$${1 \over v} = - \left( {{1 \over {3R}} + {4 \over {3H}}} \right)$$
Putting the value of Eq. (ii) h < < H
$${1 \over v} = - \left[ {{4 \over {3H}}\left( {1 + {{3H} \over 4}{{{\omega ^2}} \over {39}}} \right)} \right]$$
$$v = - \left[ {{{3H} \over 4}{{\left( {1 + {{{\omega ^2}H} \over 4}} \right)}^{ - 1}}} \right]$$
Comments (0)


