JEE Advance - Physics (2020 - Paper 2 Offline - No. 11)
Two identical non-conducting solid spheres of same mass and charge are suspended in air from a common point by two non-conducting, massless strings of same length. At equilibrium, the angle between the strings is $$\alpha$$. The spheres are now immersed in a dielectric liquid of density 800 kg m$$-$$3 and dielectric constant 21. If the angle between the strings remains the same after the immersion, then
electric force between the spheres remains unchanged
electric force between the spheres reduces
mass density of the spheres is 840 kg m$$-$$3
the tension in the strings holding the spheres remains unchanged
Explanation
In air,
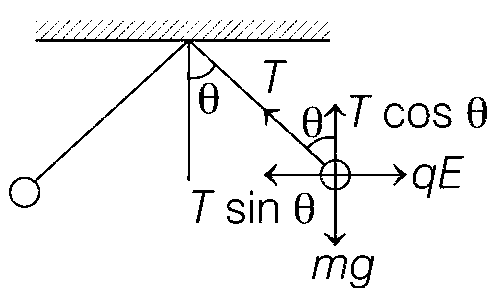
T cos$$\theta$$ = mg ..... (i)
T sin$$\theta$$ = qE ..... (ii)
qE = mg tan$$\theta$$ ..... (iii)
In liquid,
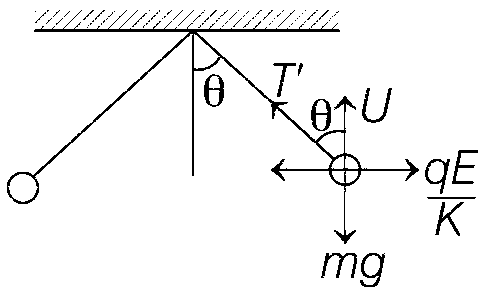
T' cos$$\theta$$ = mg $$-$$ U
T' cos$$\theta$$ = mg - $$\rho $$vg ..... (iv)
T' sin$$\theta$$ = $${{qE} \over K}$$ ...... (v)
Dividing Eq. (v) by Eq. (ii), we get
$${{T'} \over T} = {1 \over K} \Rightarrow T' = {T \over K} = {T \over {21}}$$ ..... (vi)
Dividing Eq. (iv) by Eq. (v), we get
$${{qE} \over K} = $$ (mg - $$\rho $$vg)tan $$\theta $$
$$qE = $$ K(mg - $$\rho $$vg)tan $$\theta $$ ..... (vii)
From Eqs. (vii) and (iii), we get
mg tan$$\theta $$ = K(mg - $$\rho $$vg)tan $$\theta $$
$$ \Rightarrow $$ m = K(m - $$\rho $$v)
$$ \Rightarrow $$ dv = K(dv - $$\rho $$v)
$$ \Rightarrow $$ d = Kd - K$$\rho $$
$$ \Rightarrow $$ d = 21d - 21$$\rho $$ [ $$ \because $$ K = 21]
$$ \Rightarrow $$ 20d = 21$$\rho $$
$$ \Rightarrow $$ 20d = 21 $$ \times $$ 800
$$ \Rightarrow $$ d = 840 kg/m3

T cos$$\theta$$ = mg ..... (i)
T sin$$\theta$$ = qE ..... (ii)
qE = mg tan$$\theta$$ ..... (iii)
In liquid,

T' cos$$\theta$$ = mg $$-$$ U
T' cos$$\theta$$ = mg - $$\rho $$vg ..... (iv)
T' sin$$\theta$$ = $${{qE} \over K}$$ ...... (v)
Dividing Eq. (v) by Eq. (ii), we get
$${{T'} \over T} = {1 \over K} \Rightarrow T' = {T \over K} = {T \over {21}}$$ ..... (vi)
Dividing Eq. (iv) by Eq. (v), we get
$${{qE} \over K} = $$ (mg - $$\rho $$vg)tan $$\theta $$
$$qE = $$ K(mg - $$\rho $$vg)tan $$\theta $$ ..... (vii)
From Eqs. (vii) and (iii), we get
mg tan$$\theta $$ = K(mg - $$\rho $$vg)tan $$\theta $$
$$ \Rightarrow $$ m = K(m - $$\rho $$v)
$$ \Rightarrow $$ dv = K(dv - $$\rho $$v)
$$ \Rightarrow $$ d = Kd - K$$\rho $$
$$ \Rightarrow $$ d = 21d - 21$$\rho $$ [ $$ \because $$ K = 21]
$$ \Rightarrow $$ 20d = 21$$\rho $$
$$ \Rightarrow $$ 20d = 21 $$ \times $$ 800
$$ \Rightarrow $$ d = 840 kg/m3
Comments (0)


