JEE Advance - Physics (2020 - Paper 2 Offline - No. 1)
A train with cross-sectional area St
is moving with speed vt
inside a long tunnel of cross-sectional
area S0 (S0 = 4St). Assume that almost all the air (density $$\rho $$) in front of the train flows back between
its sides and the walls of the tunnel. Also, the air flow with respect to the train is steady and laminar.
Take the ambient pressure and that inside the train to be p0. If the pressure in the region between the
sides of the train and the tunnel walls is p, then
p0 - p = $${7 \over {2N}}\rho v_t^2$$. The value of 𝑁 is ________.
p0 - p = $${7 \over {2N}}\rho v_t^2$$. The value of 𝑁 is ________.
Answer
9
Explanation
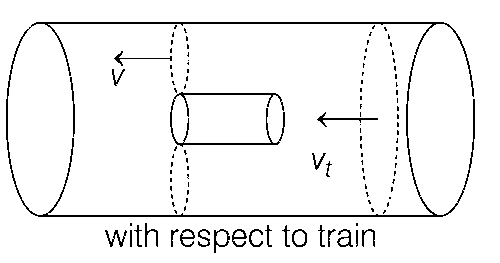
Applying Bernoulli's equation,
$${p_0} + {1 \over 2}\rho v_1^2 = p + {1 \over 2}\rho {v^2}$$
$${p_0} - p = {1 \over 2}\rho ({v^2} - v_1^2)$$ .... (i)
From equation of continuity,
$$4{S_t}{v_t} = v \times 3{S_t}$$
$$ \Rightarrow v = {4 \over 3}{v_t}$$ ..... (ii)
From Eqs. (i) and (ii), we get
$${p_0} - p = {1 \over 2}\rho \left( {{{16} \over 9}v_t^2 - v_t^2} \right) = {1 \over 2}\rho {{7v_t^2} \over 9}$$
$$\therefore$$ N = 9
Comments (0)


