JEE Advance - Physics (2020 - Paper 1 Offline - No. 8)
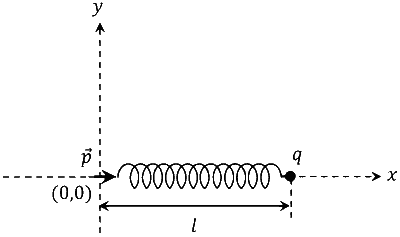
One end of a spring of negligible unstretched length and spring constant k is fixed at the origin (0, 0).
A point particle of mass m carrying a positive charge q is attached at its other end. The entire system
is kept on a smooth horizontal surface. When a point dipole $$\overrightarrow p $$ pointing towards the charge q is fixed
at the origin, the spring gets stretched to a length l and attains a new equilibrium position (see figure
below). If the point mass is now displaced slightly by $$\Delta $$l << l from its equilibrium position and
released, it is found to oscillate at frequency $${1 \over \delta }\sqrt {{k \over m}} $$. The value of $$\delta $$ is ______.

Answer
3.14
Explanation
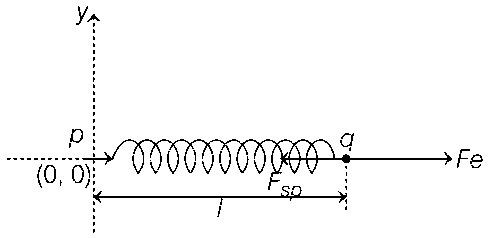
Electrostatic force = Spring force
At l, $$Fe = {F_{sp}}kl = {{2\alpha pq} \over {{l^3}}}$$ (Here, $$\alpha = {1 \over {4\pi {\varepsilon _0}}}$$)
Now, the mass m is displaced by $$\Delta $$l = x from the mean position.
$${F_{net}} = {F_{sp}} - Fe = k(l + x) - {{q(2\alpha p)} \over {{{(l + x)}^3}}}$$
$$ = k(x + 1) - {{q(2\alpha p)} \over {{l^3}{{(l + x/l)}^3}}}$$
$$ = kx + kl - q\left( {{{2\alpha p} \over {{l^3}}}} \right)\left( {1 - {{3x} \over l}} \right)$$
$$ = kx + kl - q\left( {{{2\alpha p} \over {{l^3}}}} \right) + {{2\alpha p} \over {{l^3}}}.{{3x} \over l}$$
Substituting $${{2\alpha pq} \over {{l^3}}} = kl$$, we get
$${F_{net}} = kx + kl\left( {{{3x} \over l}} \right) = 4kx$$
This is restoring in nature.
Hence, $${k_{eq}} = 4k$$
or $$T = 2\pi \sqrt {{m \over {4k}}} = \pi \sqrt {{m \over k}} $$
$$ \therefore $$ $$f = {1 \over \pi }\sqrt {{k \over m}} $$
So, $$\delta = \pi = 3.14$$
At l, $$Fe = {F_{sp}}kl = {{2\alpha pq} \over {{l^3}}}$$ (Here, $$\alpha = {1 \over {4\pi {\varepsilon _0}}}$$)

Now, the mass m is displaced by $$\Delta $$l = x from the mean position.
$${F_{net}} = {F_{sp}} - Fe = k(l + x) - {{q(2\alpha p)} \over {{{(l + x)}^3}}}$$
$$ = k(x + 1) - {{q(2\alpha p)} \over {{l^3}{{(l + x/l)}^3}}}$$
$$ = kx + kl - q\left( {{{2\alpha p} \over {{l^3}}}} \right)\left( {1 - {{3x} \over l}} \right)$$
$$ = kx + kl - q\left( {{{2\alpha p} \over {{l^3}}}} \right) + {{2\alpha p} \over {{l^3}}}.{{3x} \over l}$$
Substituting $${{2\alpha pq} \over {{l^3}}} = kl$$, we get
$${F_{net}} = kx + kl\left( {{{3x} \over l}} \right) = 4kx$$
This is restoring in nature.
Hence, $${k_{eq}} = 4k$$
or $$T = 2\pi \sqrt {{m \over {4k}}} = \pi \sqrt {{m \over k}} $$
$$ \therefore $$ $$f = {1 \over \pi }\sqrt {{k \over m}} $$
So, $$\delta = \pi = 3.14$$
Comments (0)


