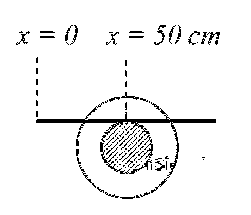
JEE Advance - Physics (2020 - Paper 1 Offline - No. 1)
A small roller of diameter 20 cm has an axle of diameter 10 cm (see figure below on the left). It is
on a horizontal floor and a meter scale is positioned horizontally on its axle with one edge of the scale
on top of the axle (see figure on the right). The scale is now pushed slowly on the axle so that it
moves without slipping on the axle, and the roller starts rolling without slipping. After the roller has
moved 50 cm, the position of the scale will look like (figures are schematic and not drawn to scale)
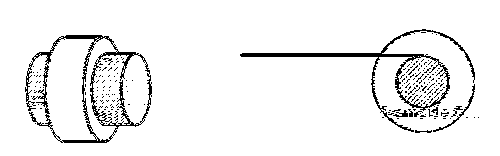
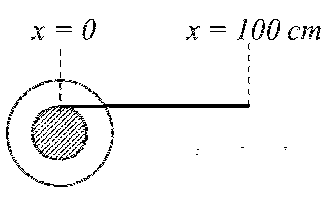
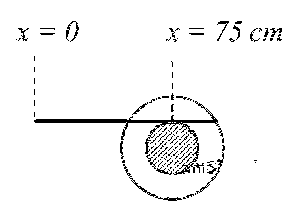
Explanation
For no slipping at ground,
vc = $$\omega $$R
(where, r is the radius of roller)
$$ \therefore $$ Velocity of scale = (vc + $$\omega $$r) (where, r is the radius of axle)
Given, vc . t = 50 cm
$$ \therefore $$ Distance moved by scale = (vc + $$\omega $$r)t = $$\left( {{v_c} + {{{v_c}r} \over r}} \right)t = {{3{v_c}} \over 2}.t = 75cm$$
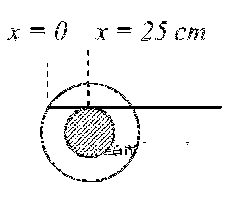
Therefore, relative displacement (with respect to centre of roller) is (75 $$-$$ 50) cm = 25 cm.
vc = $$\omega $$R
(where, r is the radius of roller)
$$ \therefore $$ Velocity of scale = (vc + $$\omega $$r) (where, r is the radius of axle)
Given, vc . t = 50 cm
$$ \therefore $$ Distance moved by scale = (vc + $$\omega $$r)t = $$\left( {{v_c} + {{{v_c}r} \over r}} \right)t = {{3{v_c}} \over 2}.t = 75cm$$
Therefore, relative displacement (with respect to centre of roller) is (75 $$-$$ 50) cm = 25 cm.
Comments (0)


