JEE Advance - Physics (2019 - Paper 1 Offline - No. 9)
In the circuit shown, initially there is no charge on the capacitors and keys S1 and S2 are open. The values of the capacitors are C1 = 10$$\mu $$F, C2 = 30$$\mu $$F and C3 = C4 = 80$$\mu $$F.
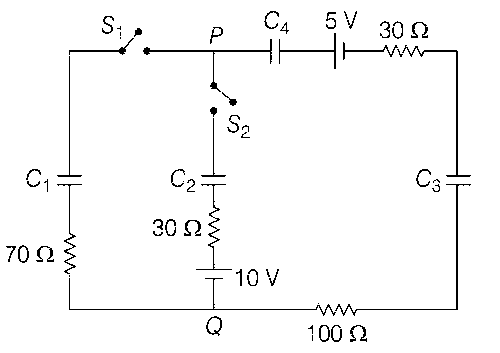
Which of the statement(s) is/are correct?

Which of the statement(s) is/are correct?
The key S1 is kept closed for long time such that capacitors are fully charged. Now, key S2 is closed, at this time, the instantaneous current across 30$$\Omega $$ resistor (between points P and Q) will be 0.2 A (round off to 1st decimal place).
If key S1 is kept closed for long time such that capacitors are fully charged, the voltage across the capacitor C1 will be 4V.
At time t = 0, the key S1 is closed, the instantaneous current in the closed circuit will be 25 mA.
If key S1 is kept closed for long time such that the capacitors are fully charged, the voltage difference between points P and Q will be 10 V.
Explanation
Just after closing of switch charge on any capacitor is zero.
$$ \therefore $$ Replace all capacitors by conducting wires.
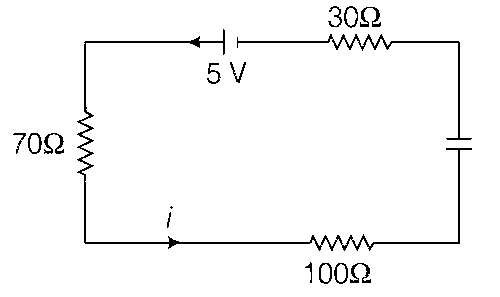
Current flow in the circuit,
$$i = {5 \over {70 + 100 + 30}} = {5 \over {200}} = 25$$ mA
Now S1 is kept closed for long time circuit is in steady state.
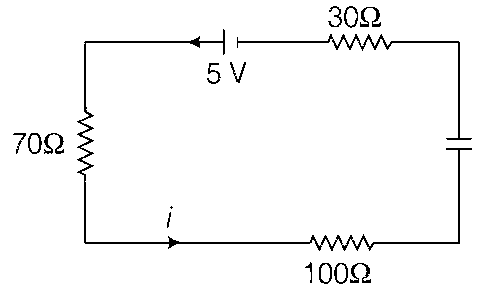
$${q \over {10}} + {q \over {80}} + {q \over {80}} - 5 = 0 \Rightarrow {{10q} \over {80}} = 5$$
$$ \therefore $$ $$q = 40\mu C$$
$$ \therefore $$ V across $${C_1} = {{40} \over {10}} = 4V$$
Now just after closing S2 charge on each capacitor remains same.
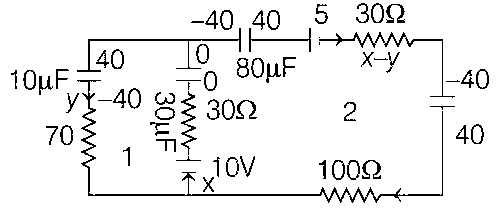
Applying KVL,
$$ - 10 + x \times 30 + {{40} \over {10}} + y \times 70 = 0$$
30x + 70y = 6 .....(1)
$$ - {{40} \over {80}} + 5 + (x - y)30 - {{40} \over {80}} + (x + y) \times 100 - 10 + x \times 30 = 0$$
$$160x - 130y - 6 = 0$$ .... (2)
$$y = {{96} \over {1510}}$$
x = 0.05 A
$$ \therefore $$ Replace all capacitors by conducting wires.

Current flow in the circuit,
$$i = {5 \over {70 + 100 + 30}} = {5 \over {200}} = 25$$ mA
Now S1 is kept closed for long time circuit is in steady state.

$${q \over {10}} + {q \over {80}} + {q \over {80}} - 5 = 0 \Rightarrow {{10q} \over {80}} = 5$$
$$ \therefore $$ $$q = 40\mu C$$
$$ \therefore $$ V across $${C_1} = {{40} \over {10}} = 4V$$
Now just after closing S2 charge on each capacitor remains same.

Applying KVL,
$$ - 10 + x \times 30 + {{40} \over {10}} + y \times 70 = 0$$
30x + 70y = 6 .....(1)
$$ - {{40} \over {80}} + 5 + (x - y)30 - {{40} \over {80}} + (x + y) \times 100 - 10 + x \times 30 = 0$$
$$160x - 130y - 6 = 0$$ .... (2)
$$y = {{96} \over {1510}}$$
x = 0.05 A
Comments (0)


