JEE Advance - Physics (2019 - Paper 1 Offline - No. 8)
One mole of a monatomic ideal gas goes through a thermodynamic cycle, as shown in the volume versus temperature (V-T) diagram. The correct statement(s) is/are [R is the gas constant]
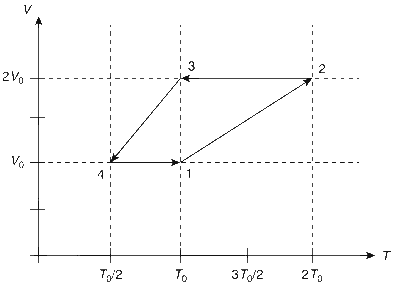

Work done in this thermodynamic cycle (1$$ \to $$2$$ \to $$3$$ \to $$4$$ \to $$1) is $$\left| W \right| = {1 \over 2}R{T_0}$$.
The ratio of heat transfer during processes 1$$ \to $$2 and 2$$ \to $$3 is $$\left| {{{{Q_{1 \to 2}}} \over {{Q_{2 \to 3}}}}} \right| = {5 \over 3}$$
The above thermodynamic cycle exhibits only isochoric and adiabatic processes.
The ratio of heat transfer during processes 1$$ \to $$2 and 3$$ \to $$4 is $$\left| {{{{Q_{1 \to 2}}} \over {{Q_{3 \to 4}}}}} \right| = {1 \over 2}$$
Explanation
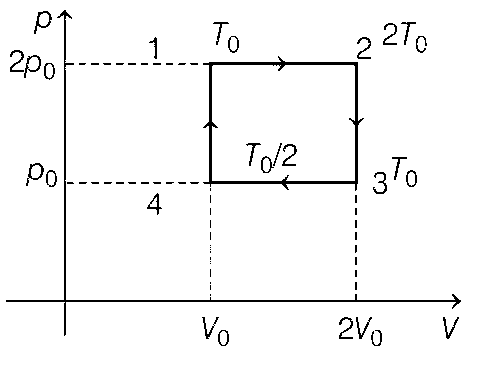
P-V graph of the given V-T graph is shown below.
(d) $$\left| {{{\Delta {Q_{1 \to 2}}} \over {\Delta {Q_{3 \to 4}}}}} \right| = \left| {{{N{C_p}\Delta {T_{1 \to 2}}} \over {N{C_p}\Delta {T_{3 \to 4}}}}} \right| = {{{T_0}} \over {{T_0}/2}} = 2$$
(b) $$\left| {{{\Delta {Q_{1 \to 2}}} \over {\Delta {Q_{2 \to 3}}}}} \right| = \left| {{{N{C_p}\Delta {T_{1 \to 2}}} \over {N{C_p}\Delta {T_{3 \to 4}}}}} \right| = {{{C_p}} \over {{C_V}}} = {5 \over 3}$$
(a) $${W_{cycle}} = {p_0}{V_0} = nR\left[ {{{{T_0}} \over 2}} \right]$$
Note For ideal gas equation,
pV = nRT
$$ \therefore $$ (pV)4 = (nRT)4
or p0V0 = $$nR{{{T_0}} \over 2}$$ = $$R{{{T_0}} \over 2}$$
as n = 1
(c) Wrong as no adiabatic process is involved.

(d) $$\left| {{{\Delta {Q_{1 \to 2}}} \over {\Delta {Q_{3 \to 4}}}}} \right| = \left| {{{N{C_p}\Delta {T_{1 \to 2}}} \over {N{C_p}\Delta {T_{3 \to 4}}}}} \right| = {{{T_0}} \over {{T_0}/2}} = 2$$
(b) $$\left| {{{\Delta {Q_{1 \to 2}}} \over {\Delta {Q_{2 \to 3}}}}} \right| = \left| {{{N{C_p}\Delta {T_{1 \to 2}}} \over {N{C_p}\Delta {T_{3 \to 4}}}}} \right| = {{{C_p}} \over {{C_V}}} = {5 \over 3}$$
(a) $${W_{cycle}} = {p_0}{V_0} = nR\left[ {{{{T_0}} \over 2}} \right]$$
Note For ideal gas equation,
pV = nRT
$$ \therefore $$ (pV)4 = (nRT)4
or p0V0 = $$nR{{{T_0}} \over 2}$$ = $$R{{{T_0}} \over 2}$$
as n = 1
(c) Wrong as no adiabatic process is involved.
Comments (0)


