JEE Advance - Physics (2019 - Paper 1 Offline - No. 7)
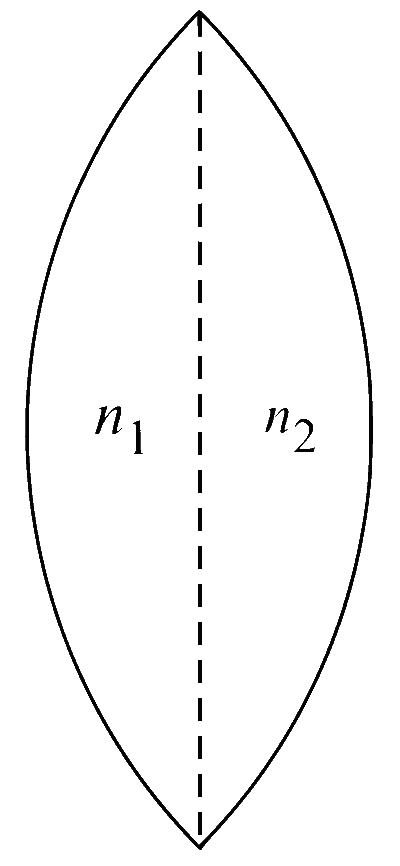
A thin convex lens is made of two materials with refractive indices n1 and n2, as shown in the figure. The radius of curvature of the left and right spherical surfaces are equal. f is the focal length of the lens when n1 = n2 = n. The focal length is f + $$\Delta $$f when n1 = n and n2 = n + $$\Delta $$n.
Assuming $$\Delta $$n << (n - 1) and 1 < n < 2, the correct statement(s) is/are
Assuming $$\Delta $$n << (n - 1) and 1 < n < 2, the correct statement(s) is/are

If $${{\Delta n} \over n} < 0$$ then $${{\Delta f} \over f}$$ > 0
For n = 1.5, $$\Delta $$n = 10-3 and f = 20 cm, the value of $$\left| {\Delta f} \right|$$ will be 0.02 cm (round off to 2nd decimal place).
$$\left| {{{\Delta f} \over f}} \right| < \left| {{{\Delta n} \over n}} \right|$$
The relation between $${{{\Delta f} \over f}}$$ and $${{{\Delta n} \over n}}$$ remains unchanged if both the convex surfaces are replaced by concave surfaces of the same radius of curvature.
Explanation
Given, thin convex lens made of two materials.
Radius of curvature of left spherical surface $=$ radius of curvature of right spherical surface
When $n_1=n_2=n$, focal length $=f$
When $n_1=n$ and $n_2=n+\Delta n$, focal length $=f+\Delta f$
Here, $\Delta n \ll(n-1)$ and $1< n < 2$
Now, when $n_1=n_2=n$, from lens maker's formula
$$ \begin{aligned} \frac{1}{f} & =(n-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)=(n-1)\left(\frac{1}{R}-\frac{1}{(-R)}\right) \\\\ \Rightarrow \frac{1}{f} & =(n-1)\left(\frac{2}{R}\right) ........(1) \end{aligned} $$
When $n_1=n$ and $n_2=n+\Delta n$
$$ \frac{1}{f+\Delta f}=(n-1) \frac{1}{R_1}-(n+\Delta n-1) \frac{1}{+R_2} $$
$$ \begin{aligned} & \quad=(n-1) \frac{1}{R}-(n+\Delta n-1) \frac{1}{(-R)} \\\\ & \Rightarrow \frac{1}{f+\Delta f}=\frac{1}{R}(n-1+n+\Delta n-1)=\frac{1}{R}(2 n+\Delta n-2) \\\\ & \Rightarrow \frac{1}{f+\Delta f}=\frac{1}{R}(2 n+\Delta n-2) ........(2) \end{aligned} $$
Subtracting Eq. (2) from Eq. (1), we get
$$ \begin{aligned} & \frac{1}{f}-\frac{1}{f+\Delta f}=(n-1)\left(\frac{2}{R}\right)-\frac{1}{R}(2 n+\Delta n-2) \\\\ & =\frac{1}{R}(2 n-2-2 n-\Delta n+2)=-\frac{\Delta n}{R} \\\\ & \Rightarrow \frac{1}{f}-\frac{1}{f+\Delta f}=-\frac{\Delta n}{R} \Rightarrow \frac{(f+\Delta f)-f}{f(f+\Delta f)}=-\frac{\Delta n}{R} \\\\ & \Rightarrow \frac{\Delta f}{f(f+\Delta f)}=-\frac{\Delta n}{R} \sim \frac{\Delta f}{f}=-\frac{\Delta n}{R} \\\\ & \Rightarrow \frac{\Delta f}{f}=-\frac{\Delta n}{R} \times f \end{aligned} $$
Using Eq. (1), we get $f=\frac{R}{2(n-1)}$
$$ \begin{aligned} & \Rightarrow \frac{\Delta f}{f}=-\frac{\Delta n}{R} \times \frac{R}{2(n-1)} \Rightarrow \frac{\Delta f}{f}=-\frac{\Delta n}{2(n-1)} \\\\ & \Rightarrow\left|\frac{\Delta f}{f}\right|=\frac{1}{2}\left|\frac{\Delta n}{n-1}\right| \\\\ & \Rightarrow\left|\frac{\Delta f}{f}\right|>\left|\frac{\Delta n}{n}\right| \end{aligned} $$
Hence, option (C) is incorrect.
Now, for $n=1.5, \Delta n=10^{-3}$ and $f=20 \mathrm{~cm}$. Using relation $\frac{\Delta f}{f(f+\Delta f)}=-\frac{\Delta n}{R}$ and Eq. (1), we get
$$ \begin{aligned} & \frac{\Delta f}{f(f+\Delta f)}=-\frac{\Delta n}{2(n-1) f} \Rightarrow \frac{\Delta f}{f+\Delta f}=-\frac{\Delta n}{2 n-2} \\\\ & \Rightarrow \Delta f(2 n-2)=-\Delta n(f+\Delta f) \\\\ & \Rightarrow \Delta f(2 n-2)=-\Delta n f-\Delta n \Delta f \\\\ & \Rightarrow \Delta f(2 n-2+\Delta n)=-\Delta n f \\\\ & \Rightarrow \Delta f=\frac{-\Delta n \times f}{2 n-2+\Delta n} \\\\ & \Rightarrow|\Delta f|=\frac{\Delta n+f}{2 n-2+\Delta n} \end{aligned} $$
Substituting all values, we get
$$ |\Delta f|=\frac{10^{-3} \times 20}{2 \times 1.5-2+10^{-3}}=0.02 \mathrm{~cm} $$
Hence, option (B) is correct.
Since $\frac{\Delta f}{f}=-\frac{\Delta n}{2(n-1)}$, so if $\frac{\Delta n}{n}<0$ then $\frac{\Delta f}{f}>0$.
Hence, option $(\mathrm{A})$ is correct.
Since the relation between $\frac{\Delta f}{f}$ and $\frac{\Delta n}{n}$ is independent of radius of curvature so the relation remains unchanged only the sign of focal length changes.
Hence, option (D) is correct.
Radius of curvature of left spherical surface $=$ radius of curvature of right spherical surface
When $n_1=n_2=n$, focal length $=f$
When $n_1=n$ and $n_2=n+\Delta n$, focal length $=f+\Delta f$
Here, $\Delta n \ll(n-1)$ and $1< n < 2$
Now, when $n_1=n_2=n$, from lens maker's formula
$$ \begin{aligned} \frac{1}{f} & =(n-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)=(n-1)\left(\frac{1}{R}-\frac{1}{(-R)}\right) \\\\ \Rightarrow \frac{1}{f} & =(n-1)\left(\frac{2}{R}\right) ........(1) \end{aligned} $$
When $n_1=n$ and $n_2=n+\Delta n$
$$ \frac{1}{f+\Delta f}=(n-1) \frac{1}{R_1}-(n+\Delta n-1) \frac{1}{+R_2} $$
$$ \begin{aligned} & \quad=(n-1) \frac{1}{R}-(n+\Delta n-1) \frac{1}{(-R)} \\\\ & \Rightarrow \frac{1}{f+\Delta f}=\frac{1}{R}(n-1+n+\Delta n-1)=\frac{1}{R}(2 n+\Delta n-2) \\\\ & \Rightarrow \frac{1}{f+\Delta f}=\frac{1}{R}(2 n+\Delta n-2) ........(2) \end{aligned} $$
Subtracting Eq. (2) from Eq. (1), we get
$$ \begin{aligned} & \frac{1}{f}-\frac{1}{f+\Delta f}=(n-1)\left(\frac{2}{R}\right)-\frac{1}{R}(2 n+\Delta n-2) \\\\ & =\frac{1}{R}(2 n-2-2 n-\Delta n+2)=-\frac{\Delta n}{R} \\\\ & \Rightarrow \frac{1}{f}-\frac{1}{f+\Delta f}=-\frac{\Delta n}{R} \Rightarrow \frac{(f+\Delta f)-f}{f(f+\Delta f)}=-\frac{\Delta n}{R} \\\\ & \Rightarrow \frac{\Delta f}{f(f+\Delta f)}=-\frac{\Delta n}{R} \sim \frac{\Delta f}{f}=-\frac{\Delta n}{R} \\\\ & \Rightarrow \frac{\Delta f}{f}=-\frac{\Delta n}{R} \times f \end{aligned} $$
Using Eq. (1), we get $f=\frac{R}{2(n-1)}$
$$ \begin{aligned} & \Rightarrow \frac{\Delta f}{f}=-\frac{\Delta n}{R} \times \frac{R}{2(n-1)} \Rightarrow \frac{\Delta f}{f}=-\frac{\Delta n}{2(n-1)} \\\\ & \Rightarrow\left|\frac{\Delta f}{f}\right|=\frac{1}{2}\left|\frac{\Delta n}{n-1}\right| \\\\ & \Rightarrow\left|\frac{\Delta f}{f}\right|>\left|\frac{\Delta n}{n}\right| \end{aligned} $$
Hence, option (C) is incorrect.
Now, for $n=1.5, \Delta n=10^{-3}$ and $f=20 \mathrm{~cm}$. Using relation $\frac{\Delta f}{f(f+\Delta f)}=-\frac{\Delta n}{R}$ and Eq. (1), we get
$$ \begin{aligned} & \frac{\Delta f}{f(f+\Delta f)}=-\frac{\Delta n}{2(n-1) f} \Rightarrow \frac{\Delta f}{f+\Delta f}=-\frac{\Delta n}{2 n-2} \\\\ & \Rightarrow \Delta f(2 n-2)=-\Delta n(f+\Delta f) \\\\ & \Rightarrow \Delta f(2 n-2)=-\Delta n f-\Delta n \Delta f \\\\ & \Rightarrow \Delta f(2 n-2+\Delta n)=-\Delta n f \\\\ & \Rightarrow \Delta f=\frac{-\Delta n \times f}{2 n-2+\Delta n} \\\\ & \Rightarrow|\Delta f|=\frac{\Delta n+f}{2 n-2+\Delta n} \end{aligned} $$
Substituting all values, we get
$$ |\Delta f|=\frac{10^{-3} \times 20}{2 \times 1.5-2+10^{-3}}=0.02 \mathrm{~cm} $$
Hence, option (B) is correct.
Since $\frac{\Delta f}{f}=-\frac{\Delta n}{2(n-1)}$, so if $\frac{\Delta n}{n}<0$ then $\frac{\Delta f}{f}>0$.
Hence, option $(\mathrm{A})$ is correct.
Since the relation between $\frac{\Delta f}{f}$ and $\frac{\Delta n}{n}$ is independent of radius of curvature so the relation remains unchanged only the sign of focal length changes.
Hence, option (D) is correct.
Comments (0)


