JEE Advance - Physics (2019 - Paper 1 Offline - No. 6)
A conducting wire of parabolic shape, initially y = x2, is moving with velocity $$v = {v_0}\widehat i$$ in a non-uniform magnetic field $$B = {B_0}\left( {1 + {{\left( {{y \over L}} \right)}^\beta }} \right)\widehat k$$, as shown in figure. If V0, B0, L and $$\beta $$ are positive constants and $$\Delta $$$$\phi $$ is the potential difference developed between the ends of the wire, then the correct statement(s) is/are
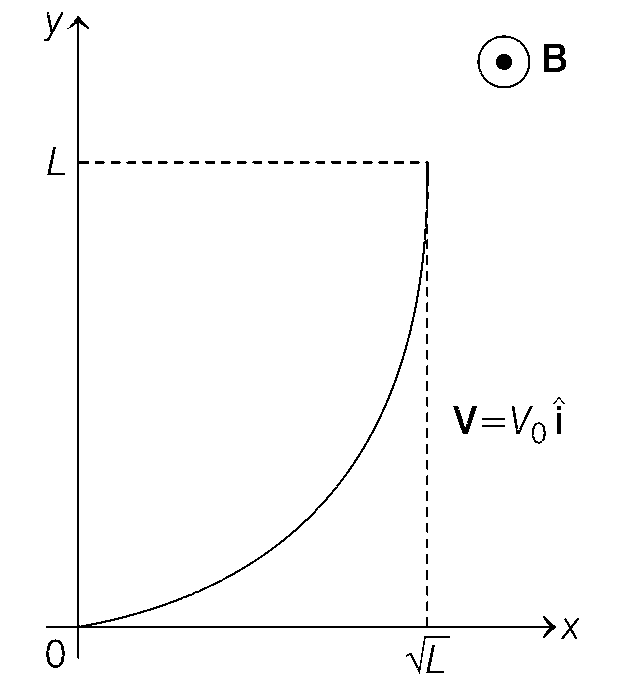

$$\left| {\Delta \phi } \right| = {4 \over 3}{B_0}{V_0}L$$ for $$\beta $$ = 2
$$\left| {\Delta \phi } \right|$$ remains the same if the parabolic wire is replaced by a straight wire, y =x initially, of length $$\sqrt 2 L$$
$$\left| {\Delta \phi } \right|$$ = $${1 \over 2}{B_0}{V_0}L$$ for $$\beta $$ = 0
$$\left| {\Delta \phi } \right|$$ is proportional to the length of the wire projected on the y-axis.
Explanation
Motional emf across the length dy is,
$$d\varepsilon = B{V_0}\,dy = {B_0}\left[ {1 + {{\left( {{y \over L}} \right)}^\beta }} \right]{V_0}dy$$
$$ \therefore $$ $$\varepsilon = \int\limits_0^L {{B_0}} \left( {1 + {{\left( {{y \over L}} \right)}^\beta }} \right){V_0}dy$$
$$ = {B_0}{V_0}\left[ {1 + {1 \over {\beta + 1}}} \right]$$
emf in loop is proportional to L for given value of $$\beta $$,
$$\beta = 0,\,\varepsilon = 2{B_0}{V_0}L$$
$$\beta = 2,\,\varepsilon = {B_0}{V_0}L\left[ {1 + {1 \over 3}} \right] = {4 \over 3}{B_0}{V_0}L$$
The length of projection of the wire Y = X of length $$\sqrt 2 L$$ on the y-axis is thus, the answer remain unchanged.
Therefore, correct options are (a), (b) and (d)
Comments (0)


