JEE Advance - Physics (2019 - Paper 1 Offline - No. 4)
Consider a spherical gaseous cloud of mass density $$\rho $$(r) in free space where r is the radial distance from its center. The gaseous cloud is made of particles of equal mass m moving in circular orbits about the common center with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If $$\rho $$(r) is constant in time, the particle number density n(r) = $$\rho $$(r)/m is [G is universal gravitational constant]
$${K \over {6\pi {r^2}{m^2}G}}$$
$${K \over {\pi {r^2}{m^2}G}}$$
$${3K \over {\pi {r^2}{m^2}G}}$$
$${K \over {2\pi {r^2}{m^2}G}}$$
Explanation
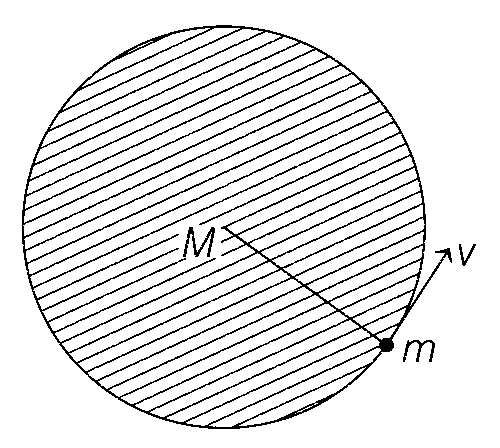
Gravitational force = Centripetal force of the earth
$${{GMm} \over {{r^2}}} = {{m{v^2}} \over r}$$
($$ \because $$ M = total mass from 0 to r)
= $${2 \over r}\left( {{1 \over 2}m{v^2}} \right)$$
$$ \Rightarrow {{GMm} \over {{r^2}}} = {{2K} \over r} \Rightarrow M = {{2Kr} \over {Gm}}$$
$$ \because $$ $$\left( {{1 \over 2}m{v^2} = K} \right)$$
Differentiate on both sides, we get
$$ \Rightarrow dM = {{2K} \over {Gm}}dr$$
$$ \Rightarrow 4\pi {r^2}dr\rho = {{2K} \over {Gm}}dr$$
($$ \because $$ volume = mass $$ \times $$ density)
$$ \therefore $$ $$\rho = {K \over {2\pi Gm{r^2}}}$$
$$ \therefore $$ $${\rho \over m} = {K \over {2\pi {r^2}{m^2}G}}$$ $$ \because $$ $$\left( {{\rho \over m} = volume} \right)$$
Comments (0)


