JEE Advance - Physics (2019 - Paper 1 Offline - No. 17)
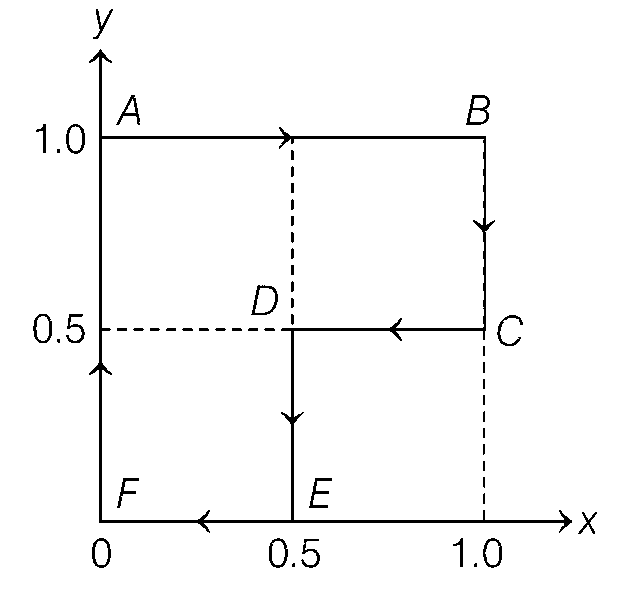
A particle is moved along a path AB-BC-CD-DE-EF-FA, as shown in figure, in presence of a force $$F = (\alpha y\widehat i + 2\alpha x\widehat j)$$ N, where x and y are in meter and $$\alpha $$ = $$ - $$1 Nm-1. The work done on the particle by this force F will be ............... Joule.

Answer
0.75
Explanation
d = F.dr
d = $$\alpha $$ydx + 2$$\alpha $$xdy
A$$ \to $$B, y = 1, dy = 0
then $${W_{A \to B}} = \int {\alpha ydx} $$$$ = \alpha 1\int_0^1 {dx} = \alpha $$
B$$ \to $$C, x = 1, dx = 0
then $${W_{B \to C}} = 2\alpha 1\int_1^{0.5} {dy} = - 2\alpha (0.5) = - \alpha $$
C$$ \to $$D, y = 0.5, dy = 0
then $${W_{C \to D}} = \int_1^{0.5} {\alpha ydx} = \alpha .{1 \over 2}\int_1^{0.5} {dx} = - {\alpha \over 4}$$
D$$ \to $$E, x = 0.5, dx = 0
then $${W_{D \to E}} = 2\alpha \int {xdy} = 2\alpha .{1 \over 2}\int\limits_{0.5}^0 {dy} = - {\alpha \over 2}$$
E$$ \to $$F, y = 0, dy = 0 then WEF = 0
F$$ \to $$A, x = 0, dx = 0 then WF$$ \to $$A = 0
$$ \therefore $$ $$W = \alpha - \alpha - {\alpha \over 4} - {\alpha \over 2} = - {{3\alpha } \over 4}$$
Given, $$\alpha = - 1 $$
$$\Rightarrow W = {3 \over 4}J = 0.75J$$
d = $$\alpha $$ydx + 2$$\alpha $$xdy
A$$ \to $$B, y = 1, dy = 0
then $${W_{A \to B}} = \int {\alpha ydx} $$$$ = \alpha 1\int_0^1 {dx} = \alpha $$
B$$ \to $$C, x = 1, dx = 0
then $${W_{B \to C}} = 2\alpha 1\int_1^{0.5} {dy} = - 2\alpha (0.5) = - \alpha $$
C$$ \to $$D, y = 0.5, dy = 0
then $${W_{C \to D}} = \int_1^{0.5} {\alpha ydx} = \alpha .{1 \over 2}\int_1^{0.5} {dx} = - {\alpha \over 4}$$
D$$ \to $$E, x = 0.5, dx = 0
then $${W_{D \to E}} = 2\alpha \int {xdy} = 2\alpha .{1 \over 2}\int\limits_{0.5}^0 {dy} = - {\alpha \over 2}$$
E$$ \to $$F, y = 0, dy = 0 then WEF = 0
F$$ \to $$A, x = 0, dx = 0 then WF$$ \to $$A = 0
$$ \therefore $$ $$W = \alpha - \alpha - {\alpha \over 4} - {\alpha \over 2} = - {{3\alpha } \over 4}$$
Given, $$\alpha = - 1 $$
$$\Rightarrow W = {3 \over 4}J = 0.75J$$
Comments (0)


